51.数组中的逆序对.md

51.数组中的逆序对

题目

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

示例 1:

输入: [7,5,6,4] 输出: 5

限制： 0 <= 数组长度 <= 50000

思路 & 解答

首先，也就是数组中任意两个数，只要前面的数大于后面的数，就是逆序对。先来一次暴力破解：遍历任意两个数，只要符合条件，总数就增加1。

class Solution {
    public int reversePairs(int[] nums) {
    int i=0, j=0, sum=0;
    for( i=0; i<nums.length; i++ ){
        for( j=i+1; j<nums.length; j++ ){
            if( nums[j] < nums[i] ) sum++;
        }
    }
    return sum;
    }
}

C++ 代码如下：

class Solution {
public:
    int InversePairs(vector<int> nums) {
        int i = 0, j = 0, sum = 0;
        for (i = 0; i < nums.size(); i++) {
            for (j = i + 1; j < nums.size(); j++) {
                if (nums[j] < nums[i]) sum++;
            }
        }
        return sum;
    }
};

毫无疑问，这个时间复杂度是O(n²),肯定会超时。

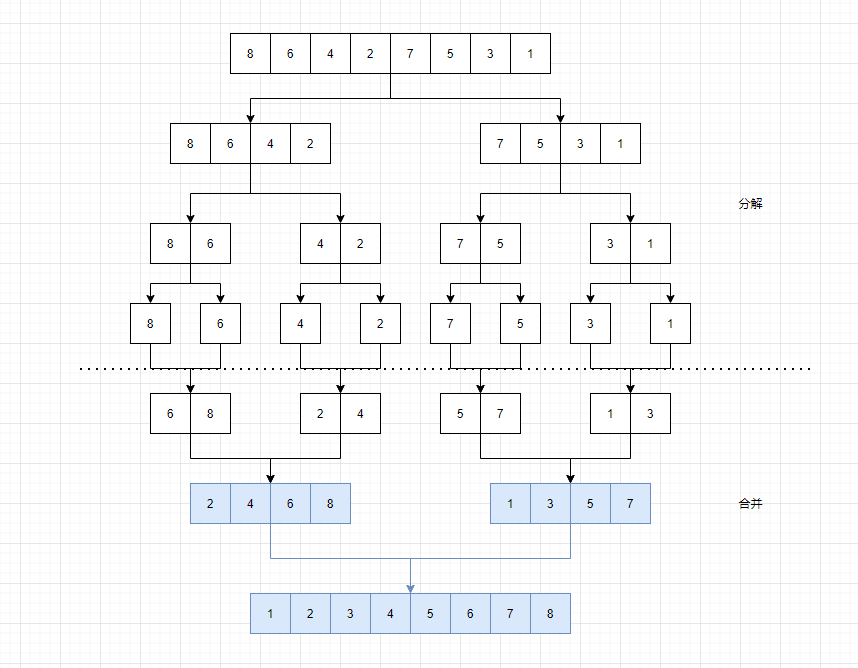
第二种方法就是利用分治的思想，在归并排序的基础上稍微改动即可。以数组[8,6,4,2,7,5,3,1]为例：

我们可以发现，其实在合并的过程中，两个有序的数组，可以直接计算出逆序数组的个数。我们以[8,6,4,2,7,5,3,1]，实际上分为[8,6,4,2]和[7,5,3,1]，逆序的个数为第一部分[8,6,4,2]中的逆序个数+第二部分[7,5,3,1]中的逆序个数，还有第三部分是[8,6,4,2]中的元素相对[7,5,3,1]的逆序个数。

分为两半之后的逆序个数，一看就是分治法，递归即可，而两部分的相对逆序，我们可以在合并有序数组的时候得出。

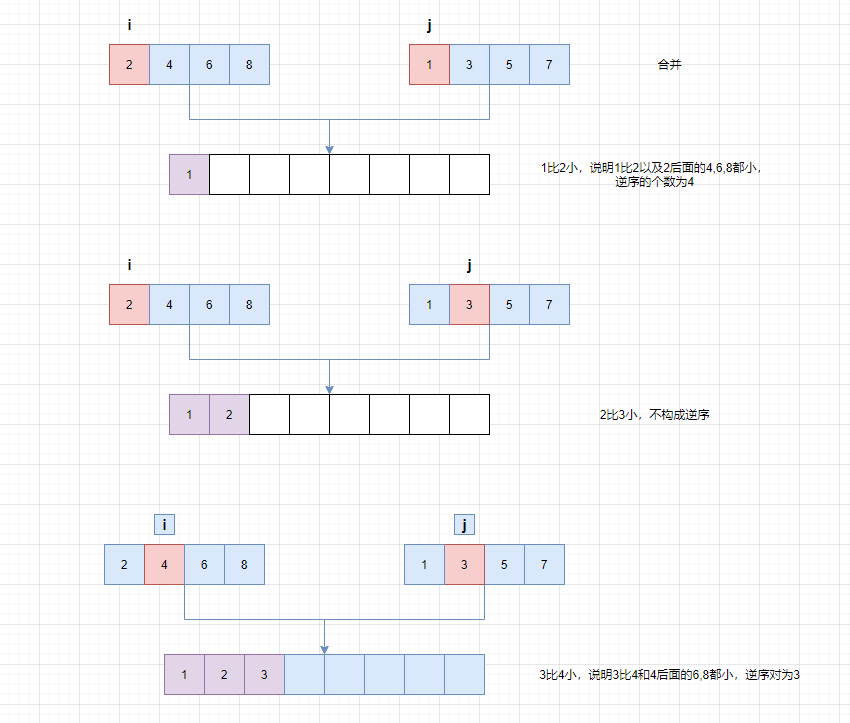
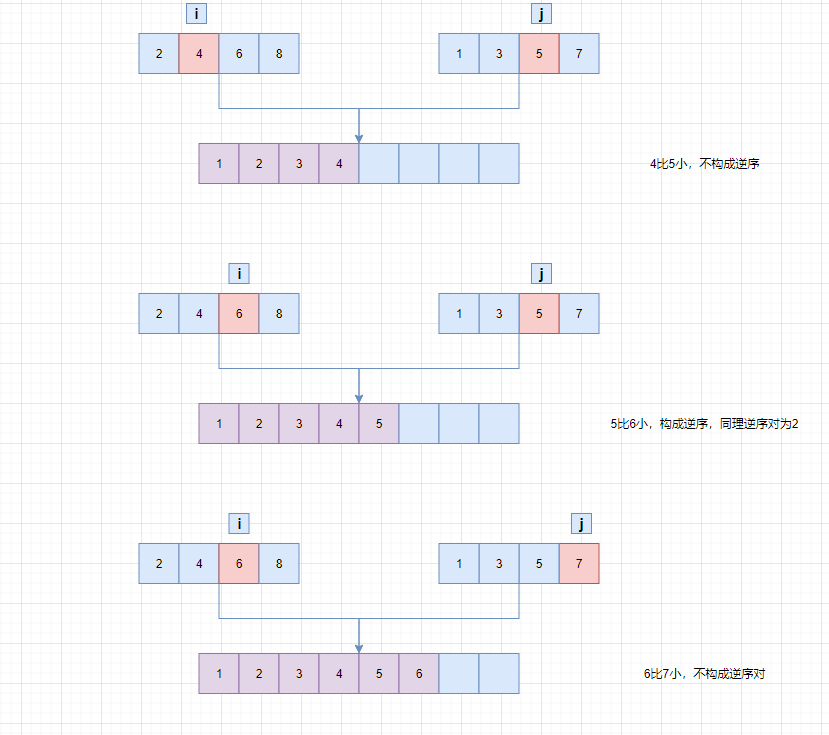
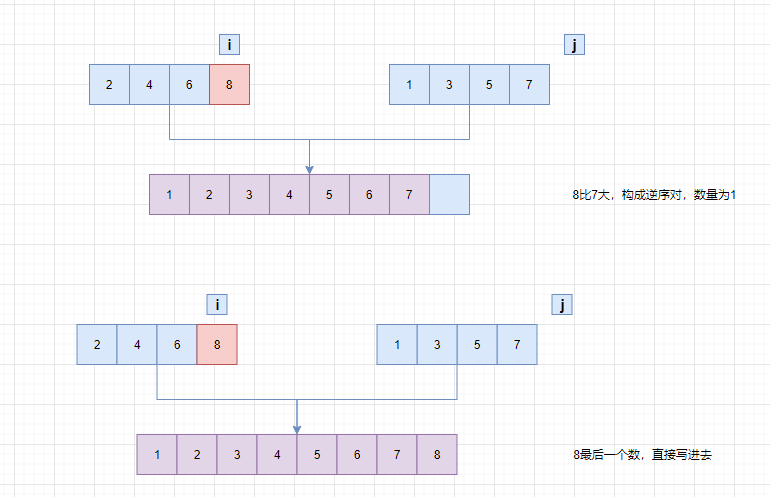
合并的时候使用双指针，i指向第一个数组的第一个元素，j指向第二个数组的第一个元素。哪一个元素小，就将该元素写入新的数组中，同时指针后移。

如果第二个数组中的元素小于第一个数组中的元素，那么就构成了逆序对，逆序对的个数：如果中间分隔是索引是mid，那么构成逆序对的个数为mid-i+1。

代码如下：

public class Solution35 {
    public static void main(String[] args) {
        int[] nums = {8, 6, 4, 2, 7, 5, 3, 1};
        Solution35 solution35 = new Solution35();
        int result = solution35.InversePairs(nums);
        System.out.println(result);
    }

    public int InversePairs(int[] array) {
        if (array == null || array.length < 2) {
            return 0;
        }
        int[] nums = new int[array.length];
        return getNums(array, nums, 0, array.length - 1) % 1000000007;
    }

    public int getNums(int[] array, int[] nums, int left, int right) {
        if (left >= right) {
            return 0;
        }
        int mid = left + (right - left) / 2;
        int leftNum = getNums(array, nums, left, mid) % 1000000007;
        int rightNum = getNums(array, nums, mid + 1, right) % 1000000007;
        return leftNum + rightNum + mergeNum(array, nums, left, mid, right);
    }

    public int mergeNum(int[] array, int[] nums, int left, int mid, int right) {
        for (int i = left; i <= right; i++) {
            nums[i] = array[i];
        }
        int count = 0;
        int i = left, j = mid + 1;
        for (int k = left; k <= right; k++) {
            if (i == mid + 1) {
                array[k] = nums[j];
                j++;
            } else if (j == right + 1) {
                array[k] = nums[i];
                i++;
            } else if (nums[i] <= nums[j]) {
                array[k] = nums[i];
                i++;
            } else {
                array[k] = nums[j];
                j++;
                count = (count + (mid - i + 1)) % 1000000007;
            }
        }
        return count % 1000000007;
    }
}

C++ 代码如下：

class Solution {
public:
    int InversePairs(vector<int> array) {
        if (array.size() < 2) {
            return 0;
        }
        vector<int> nums(array.size());
        return getNums(array, nums, 0, array.size() - 1) % 1000000007;
    }

    int getNums(vector<int> &array, vector<int> &nums, int left, int right) {
        if (left >= right) {
            return 0;
        }
        int mid = left + (right - left) / 2;
        int leftNum = getNums(array, nums, left, mid) % 1000000007;
        int rightNum = getNums(array, nums, mid + 1, right) % 1000000007;
        return leftNum + rightNum + mergeNum(array, nums, left, mid, right);
    }

    int mergeNum(vector<int>&array, vector<int> &nums, int left, int mid, int right) {
        for (int i = left; i <= right; i++) {
            nums[i] = array[i];
        }
        int count = 0;
        int i = left, j = mid + 1;
        for (int k = left; k <= right; k++) {
            if (i == mid + 1) {
                array[k] = nums[j];
                j++;
            } else if (j == right + 1) {
                array[k] = nums[i];
                i++;
            } else if (nums[i] <= nums[j]) {
                array[k] = nums[i];
                i++;
            } else {
                array[k] = nums[j];
                j++;
                count = (count + (mid - i + 1)) % 1000000007;
            }
        }
        return count % 1000000007;
    }
};

时间复杂度同归并排序的时间复杂度，也就是O(nlogn)，空间复杂度，由于临时需要使用一个数组，所以为O(n)。

有一个很坑的地方：只要涉及到加和的地方都有可能溢出，一旦溢出就会导致结果出错，数据量大，很难调试。凡是涉及到加和的地方都要 % 1000000007。真的很迷...