Skip to content

Latest commit

 

History

History
530 lines (406 loc) · 37.7 KB

Bayesian learning.md

File metadata and controls

530 lines (406 loc) · 37.7 KB

Bayesian Learning and Probabilistic Programming

Bayesian learning can be regarded as the extension of Bayesian statistics. The core topic of Bayesian learning is thought as prior information to explain the uncertainty of parameters. It is related with Bayesian statistics, computational statistics, probabilistic programming and machine learning.

model_based_clustering

Bayes Formulae Inverse Bayes Formulae
$f_X(x)=\frac{f_{X, Y}(X, Y)}{f_{Y\mid X}(y\mid x)}=\frac{f_{X\mid Y}(x\mid y)f_Y(y)}{f_{Y\mid X}(y\mid x)}$ $f_X(x) = (\int_{S_y} \frac{ f_{Y\mid X}(y\mid x)}{f_{X\mid Y}(x\mid y)}\mathrm{d}y)^{-1}$
$f_X(x)\propto f_{X\mid Y}(x\mid y)f_Y(y)(=f_{X, Y}(X, Y))$ $f_X(x) \propto \frac{f_{X\mid Y}(x\mid y_0)}{f_{Y\mid X}(y_0\mid x)}$

Naive Bayes

Naive Bayes is to reconstruct the joint distribution of features and labels $Pr(\vec{x}, y)$ given some training dataset/samples $T={(\vec{X}i, y_i)}{i=1}^{n}$. However, the features are usually in high dimensional space in practice so the dimension curse occurs which makes it impossible to compute the joint distribution $Pr(\vec{X}, y)$ via the (emprical) conditional probability $Pr(\vec{X}\mid y)$ and the prior $Pr(y)$. A naive idea is to simplify the computation process by assumption that the features are conditional independence so that $$ Pr(\vec{X}\mid y) =\prod_{i=1}^{p} Pr(\vec{X}^{(i)}\mid y).\tag{1} $$

And the predicted labels will be computed via $$ Pr(y\mid \vec{X}) = \frac{Pr(y) Pr(\vec{x}\mid y)}{\sum Pr(y)Pr(\vec{x}\mid y)}. \tag{2} $$

where the conditional probability $Pr(\vec{X}\mid y)$ is simplified by the conditional independence assumption in formula (1). Thus the naive Bayes classifier is represented as maximum a posteriori (MAP) $$ y=f(x)=\arg_{y} Pr(y\mid \vec{X}). $$

The prior probability $Pr(y)$ can be emprical or estimated.

Gaussian Naive Bayes

Average One-Dependence Estimator (AODE)

Approximate Bayesian Inference

Approximate Rejection Algorithm:

  1. Draw $\theta$ from $\pi(\theta)$;
  2. Simulate $D′ \sim P(\cdot\mid \theta)$;
  3. Accept $\theta$ if $\rho(D, D')\leq \epsilon$.

Expectation propagation

Variational Bayes Methods

Variational inference is an umbrella term for algorithms which cast posterior inference as optimization.

Hierarchical Models

We consider a multilevel model to be a regression (a linear or generalized linear model) in which the parameters—the regression coefficients—are given a probability model. This second-level model has parameters of its own—the hyperparameters of the model—which are also estimated from data. The two key parts of a multilevel model are varying coefficients, and a model for those varying coefficients (which can itself include group-level predictors). Classical regression can sometimes accommodate varying coefficients by using indicator variables. The feature that distinguishes multilevel models from classical regression is in the modeling of the variation between groups.

Multilevel models are also called hierarchical, for two different reasons: first, from the structure of the data (for example, students clustered within schools); and second, from the model itself, which has its own hierarchy, with the parameters of the within-school regressions at the bottom, controlled by the hyperparameters of the upper-level model.

Hierarchical Bayesian Regression

Hierarchical  Bayes：

  • explicitly  represent  category  hierarchies  for sharing  abstract  knowledge.
  • explicitly  idenAfy  only  a  small  number  of parameters  that  are  relevant  to  the  new concept  being  learned. Hierarchical Bayesian Regression extends the Bayesian models by setting the uncertainty of the uncertainty such as $$ y\sim Pr(\phi(x)\mid \theta)\ Pr(\phi(x)\mid \theta) = \frac{Pr(\theta\mid\phi(x))Pr(\phi(x))}{P(\theta)}\ Pr(\phi(x))= Pr(\phi(x)\mid \eta) Pr(\eta)\ \vdots $$

We can take any factor into consideration in this hierarchical Bayesian model. And it is a graphical probability model, which consists of the connections and probability.

Beta-logistic

Assume that the instantaneous event probability at time step t is characterized by a geometric distribution: $$P(T=t\mid \theta)=\theta(1-\theta).$$

Instead of a point estimate for $\theta$, use a Beta prior parameterized as follows: $$\alpha(x)=\exp(a(x)), \beta(x)=\exp(b(x)).$$ The likelihood function is $$L(\alpha, \beta)=\prod_{i,,,, observed} P(T=t_i\mid \alpha(x_i), \beta(x_i))\prod_{i,,, censored} P(T> t_i\mid \alpha(x_i), \beta(x_i) ).$$

Nice properties:

  • $P(T=1\mid \alpha, \beta)=\frac{\alpha}{\alpha + \beta}$;
  • $P(T=t\mid \alpha, \beta)=(\frac{\beta + t - 2}{\alpha + \beta+t-1})P(T=t-1\mid \alpha, \beta)$.

If $a$ and $b$ are linear: $a(x)=\gamma_a\cdot x$ and $b(x)=\gamma_b \cdot x$, then $$P(T=1\mid \alpha, \beta)=\frac{\alpha(x)}{\alpha(x) + \beta(x)}=\frac{1}{1+\exp(\left<\gamma_a-\gamma_b, x\right>)}.$$

For $T=1$, it reduces to overparameterized logistic regression.

Latent Dirichlet Allocation

Latent Dirchlet Allocation(LDA) is a topic model in natural language processing.

Generative  Process: $w \sim LDA$:

  • Draw each topic $\theta_k \sim Dir(\eta)$ for $k=1,\cdots, K$.
  • For each document:
    • Draw topic proportions $\pi_d \sim Dir(\alpha)$
    • For each word:
      • Draw topic indicator $z_{d, n} \sim Mult(\pi_d)$
      • Draw word $w_{d, n} \sim Mult(\theta_{z_d, n})$

Hierarchical  Generative  Model

Optimal Learning

The Bayesian perspective casts a different interpretation on the statistics we compute, which is particularly useful in the context of optimal learning. In the frequentist perspective, we do not start with any knowledge about the system before we have collected any data. By contrast, in the Bayesian perspective we assume that we begin with a prior distribution of belief about the unknown parameters.

Everyday decisions are made without the benefit of accurate information. Optimal Learning develops the needed principles for gathering information to make decisions, especially when collecting information is time-consuming and expensive. Optimal learning addresses the problem of efficiently collecting information with which to make decisions. Optimal learning is an issue primarily in applications where observations or measurements are expensive.

It is possible to approach the learning problem using classical and familiar ideas from optimization. The operations research community is very familiar with the use of gradients to minimize or maximize functions. Dual variables in linear programs are a form of gradient, and these are what guide the simplex algorithm. Gradients capture the value of an incremental change in some input such as a price, fleet size or the size of buffers in a manufacturing system. We can apply this same idea to learning.

There is a list of optimal learning problems.

Bayesian Optimization

Bayesian optimization has been successful at global optimization of expensive-to-evaluate multimodal objective functions. However, unlike most optimization methods, Bayesian optimization typically does not use derivative information.

As response surface methods, they date back to Box and Wilson in 1951. Bayesian optimization usually uses Gaussian process regression.

Bayesian Ensemble Methods

Bayesian parameter averaging

Bayesian parameter averaging (BPA) is an ensemble technique that seeks to approximate the Bayes optimal classifier by sampling hypotheses from the hypothesis space, and combining them using Bayes' law.

Bayesian model combination

Bayesian model combination (BMC) is an algorithmic correction to Bayesian model averaging (BMA). Instead of sampling each model in the ensemble individually, it samples from the space of possible ensembles (with model weightings drawn randomly from a Dirichlet distribution having uniform parameters). This modification overcomes the tendency of BMA to converge toward giving all of the weight to a single model.

Bayesian Committe Machine

The Bayesian committee machine (BCM) is a novel approach to combining estimators which were trained on different data sets. Although the BCM can be applied to the combination of any kind of estimators the main foci are Gaussian process regression and related systems such as regularization networks and smoothing splines for which the degrees of freedom increase with the number of training data. Somewhat surprisingly, we find that the performance of the BCM improves if several test points are queried at the same time and is optimal if the number of test points is at least as large as the degrees of freedom of the estimator. The BCM also provides a new solution for online learning with potential applications to data mining. We apply the BCM to systems with fixed basis functions and discuss its relationship to Gaussian process regression. Finally, we also show how the ideas behind the BCM can be applied in a non-Bayesian setting to extend the input dependent combination of estimators.

Objective Bayes Methodology

Probabilistic Graphical Model

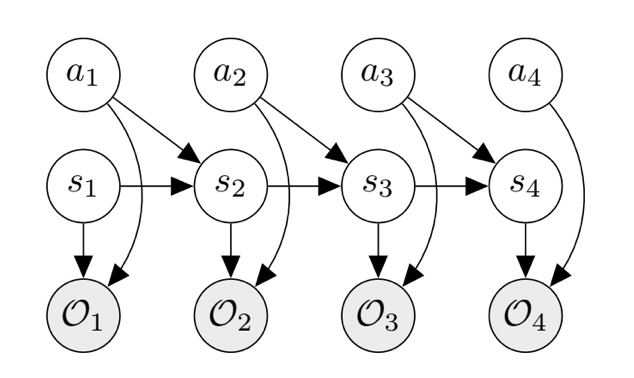
A graphical model or probabilistic graphical model (PGM) or structured probabilistic model is a probabilistic model for which a graph expresses the conditional dependence structure between random variables. They are commonly used in probability theory, statistics — particularly Bayesian statistics — and machine learning. It is a marriage of graph theory and probability theory. It is aimed to solve the causal inferences, which is based on principles rather than models.

Bayesian Belief Network(BBN)

Bayesian Network

Bayesian networks are a type of Probabilistic Graphical Model that can be used to build models from data and/or expert opinion. They are also commonly referred to as Bayes nets, Belief networks and sometimes Causal networks.

Bayesian Network (BN) is an intuitive, graphical representation of a joint probability distribution of a set of random variables with a possible mutual causal relationship.

It is of wide application in many fields such as NLP, medical image analysis.

Hidden Markov Models

A HMM $\lambda$ is a sequence made of a combination of 2 stochastic processes:

  • the probability of a particular state depends only on the previous state: $$Pr(q_i\mid q_1, \dots, q_{i-1}) = Pr(q_i \mid q_{i-1});$$
  • the probability of an output observation $o_i$ depends only on the state that produced the observation $q_i$ and not on any other states or any other observations: $$Pr(o_i\mid q_1, \dots, q_{i-1}, o_1, \cdots, o_{i-1}) = Pr(o_i \mid q_{i}).$$

A HMM model is defined by :

  • the vector of initial probabilities $\pi = [ {\pi}_1, ... {\pi}_q ]$ where $\pi_i = Pr(q_1 = i)$.
  • a transition matrix for unobserved sequence ${A}$: $A = [a_{ij}] = Pr(q_t = j \mid q_{t-1} = i)$.
  • a matrix of the probabilities of the observations: $B = [b_{ki}] = Pr(o_t = s_k \mid q_t = i)$.

The hidden Markov models should be characterized by three fundamental problems:

  1. (Likelihood): Given an HMM $\lambda = (A,B)$ and an observation sequence ${O}$, determine the likelihood $Pr(O|\lambda)$.
  2. (Decoding): Given an observation sequence ${O}$ and an HMM $\lambda = (A,B)$, discover the best hidden state sequence ${Q}$.
  3. (Learning): Given an observation sequence ${O}$ and the set of states in the HMM, learn the HMM parameters ${A}$ and ${B}$.

Likelihood Computation

$$ Pr(O|\lambda)=\prod_{i}\underbrace{Pr(o_i \mid q_{i})}{observed} \underbrace{Pr(q_i\mid \lambda)}{hidden}\ = \sum_{i}Pr(O, q_i\mid \lambda) $$

The forward algorithm

Forward probability is defined as $\alpha_t(i)=Pr(o_1, \cdots, o_t, q_t=i\mid \lambda)$.

  1. Initialization: $\alpha_1(i)=Pr(o_1, q_1=i\mid \lambda)=\pi_i Pr(o_1\mid q_1=i)=\pi_1 b_{o_1i}\quad\forall i$;
  2. Recursion: $\alpha_t(i)=[\sum_{j}\alpha_{t-1}(j)a_{ji}]b_{o_ti}\quad\forall i$;
  3. Termination: $Pr(O\mid \lambda)=\sum_{i}\alpha_T(i)$.

The backward algorithm

Backward probability is defined as $\beta_t(i)=Pr(o_{t+1}, o_{t+2}, \cdots, o_T\mid i_t=q, \lambda)$.

  1. Initialization: $\beta_T(i)=1,\quad i=1,2,\cdots,N$;
  2. For $t=T-1, T-2,\cdots, 1$, $$\beta_t(i)=\sum_{j=1}^Na_{ij}b_j(o_{t+1})\beta_{t+1}(j),\quad i=1,2,\cdots,N$$
  3. Termination: $Pr(O\mid \lambda)=\sum_{i}\pi_i b_i(o_1)\beta_1(i)$.

Decoding

Given an HMM $\lambda = (A,B)$ and an observation sequence ${O}$, determine the likelihood $Pr(O|\lambda)$. $$Q^{\ast}=\arg\max_{Q}Pr(O\mid \lambda)\ =\arg\max_{Q}\sum_{i}\alpha_T(i)$$

Viterbi is a kind of dynamic programming Viterbi algorithm that makes uses of a dynamic programming trellis.

Learning

Given an observation sequence ${O}$ and the set of states in the HMM, learn the HMM parameters $\lambda=(\pi, {A}, {B})$.

Baum-Welch Algorithm

$$P(O\mid \lambda)=\sum_{I}P(O\mid I)P(I\mid \lambda)$$ The state sequence is hidden variable.

Baum-Welch Algorithm is exactly an application of expectation maximum algorithm. The Q function is defined as $$Q(\lambda, \bar\lambda)=\mathbb E(\log{P(O, I\mid \lambda)})=\log{P(O, I\mid \lambda)}P(O, I\mid \bar\lambda)$$ where $\bar\lambda$ is the optimal estimation at current step.

As usual, the key step of expectation maximum is to find the $Q$ function which is easy to be maximized and it is defined in the recursive form as follows: $$\bar\lambda \leftarrow \arg\max_{\lambda}Q(\lambda, \bar\lambda).$$

Probabilistic Programming

Probabilistic graphical models provide a formal lingua franca for modeling and a common target for efficient inference algorithms. Their introduction gave rise to an extensive body of work in machine learning, statistics, robotics, vision, biology, neuroscience, artificial intelligence (AI) and cognitive science. However, many of the most innovative and useful probabilistic models published by the AI, machine learning, and statistics community far outstrip the representational capacity of graphical models and associated inference techniques. Models are communicated using a mix of natural language, pseudo code, and mathematical formulae and solved using special purpose, one-off inference methods. Rather than precise specifications suitable for automatic inference, graphical models typically serve as coarse, high-level descriptions, eliding critical aspects such as fine-grained independence, abstraction and recursion.

PROBABILISTIC PROGRAMMING LANGUAGES aim to close this representational gap, unifying general purpose programming with probabilistic modeling; literally, users specify a probabilistic model in its entirety (e.g., by writing code that generates a sample from the joint distribution) and inference follows automatically given the specification. These languages provide the full power of modern programming languages for describing complex distributions, and can enable reuse of libraries of models, support interactive modeling and formal verification, and provide a much-needed abstraction barrier to foster generic, efficient inference in universal model classes.

We believe that the probabilistic programming language approach within AI has the potential to fundamentally change the way we understand, design, build, test and deploy probabilistic systems. This approach has seen growing interest within AI over the last 10 years, yet the endeavor builds on over 40 years of work in range of diverse fields including mathematical logic, theoretical computer science, formal methods, programming languages, as well as machine learning, computational statistics, systems biology, probabilistic AI.

Graph Nets library
Graph net
There is a list of existing probabilistic programming systems at http://www.probabilistic-programming.org/wiki/Home and a list of research articles on probabilistic programming until 2015.

The Algorithms Behind Probabilistic Programming includes: Bayesian Inference, Hamiltonian Monte Carlo and the No U-Turn Sampler, Variational Inference and Automatic Differentation and Probabilistic Programming Languages.