Skip to content

Latest commit

 

History

History
668 lines (472 loc) · 40.6 KB

Geometric Deep Learning.md

File metadata and controls

668 lines (472 loc) · 40.6 KB

Geometric Deep Learning

In the last decade, Deep Learning approaches (e.g. Convolutional Neural Networks and Recurrent Neural Networks) allowed to achieve unprecedented performance on a broad range of problems coming from a variety of different fields (e.g. Computer Vision and Speech Recognition). Despite the results obtained, research on DL techniques has mainly focused so far on data defined on Euclidean domains (i.e. grids). Nonetheless, in a multitude of different fields, such as: Biology, Physics, Network Science, Recommender Systems and Computer Graphics; one may have to deal with data defined on non-Euclidean domains (i.e. graphs and manifolds). The adoption of Deep Learning in these particular fields has been lagging behind until very recently, primarily since the non-Euclidean nature of data makes the definition of basic operations (such as convolution) rather elusive. Geometric Deep Learning deals in this sense with the extension of Deep Learning techniques to graph/manifold structured data.

Images are stored in computer as matrix roughly. The spatial distribution of pixel on the screen project to us a colorful digitalized world. Convolutional neural network(ConvNet or CNN) has been proved to be efficient to process and analyses the images for visual cognitive tasks. What if we generalize these methods to graph structure which can be represented as adjacent matrix?

Image Graph
Convolutional Neural Network Graph Convolution Network
Attention Graph Attention
Gated Gated Graph Network
Generative Generative Models for Graphs

Advanced proceedings of natural language processing(NLP) shone a light into semantic embedding as one potential approach to knowledge representation. The text or symbol, strings in computer, is designed for natural people to communicate and understand based on the context or situation, i.e., the connections of entities and concepts are essential. What if we generalize these methods to connected data?

Spherical CNN

Hyperbolic Deep Learning

The hyperbolic space is different from the Euclidean space. It has more capacity. The volume of a ball grows exponentially with its radius! Think of a binary tree: the number of nodes grows exponentially with depth. Hyperbolic geometry is better suited to embed data with an underlying hierarchical/heterogeneous structure. Let’s make deep learning possible in hyperbolic space.

Recall the recursive form of forward neural network: $$ X\to \underbrace{\sigma}{nonlinerality}\circ \underbrace{(\underbrace{W_1X}{\text{Matrix-vector multiplication}}+b_1)}_{\text{Bias translation}}=H_1\to \cdots \sigma(WH+b)=y. $$

It consists of matrix-vector multiplication, vector addition, nonlinear transformation and function composition.

The hyperbolic hyperplane centered at $p\in\mathbb{D}^n$, with normal direction $a\in T_p\mathbb{D}^n$ is given by

$$\lbrace x\in\mathbb{D}^n,\ \langle (-p)\oplus x, a\rangle=0\rbrace.$$

The hyperbolic softmax probabilities are given by

$$p(y=k\mid x) \propto \exp\left(\lambda_{p_k}\parallel a_k\parallel \sinh^{-1}\left(\frac{2\langle (-p_k)\oplus x,a_k\rangle}{(1-\parallel (-p_k)\oplus x,a_k\parallel^2)\parallel a_k\parallel}\right)\right)$$ with $p_k\in\mathbb{D}^n and a_k\in T_{p_k}\mathbb{D}^n$.

Bias translation

The Möbius addition of $y$ to $x$ is defined by $$ x \oplus y :=\frac{\left(1+2(x, y)+{|y|}{2}^{2}\right) x+\left(1-{|x|}{2}^{2}\right) y}{1+2\langle x, y\rangle+{|x|}{2}^{2}{|y|}{2}} $$

$$\mathbf{x} \oplus \mathbf{y} =\frac{\left(1+2 c\langle\mathbf{x}, \mathbf{y}\rangle+ c|\mathbf{y}|^{2}\right) \mathbf{x}+\left(1-c|\mathbf{x}|^{2}\right) \mathbf{y}}{1+2 c\langle\mathbf{x}, \mathbf{y}\rangle+ c^{2}|\mathbf{x}|^{2}|\mathbf{y}|^{2} |} $$

Scalar multiplication

The Möbius scalar multiplication of $x$ by $r \in \mathbb{R}$ is defined by $$ r \otimes x=\tanh \left(r \tanh ^{-1}\left({|x|}_{2}\right)\right) \frac{x}{|x|} $$

Likewise, this operation satisfies a few properties:

  • Associativity:
    $$r \otimes(s \otimes x) = (r \otimes s) \otimes x$$
  • additions: $$ n \otimes x=x \oplus \cdots \oplus x(n \text { times })$$
  • Scalar distributivity: $$(r+s) \otimes x=(r \otimes x) \oplus(s \otimes x)$$
  • Scaling property: $$r \otimes x /|r \otimes x|=x /|x|.$$

The geodesic between two points $x,y\in\mathbb{D}^n$ is the shortest path connecting them, and is given by $$ \forall t \in[0,1], \gamma_{x \rightarrow y}(t)=x \oplus(t \otimes((-x) \oplus y)). $$ Similarly, in Euclidean space, the shortest path between two points $x,y\in\mathbb{R}^n$ is given by $$ \forall t \in[0,1], \gamma_{x \rightarrow y}(t)=x + (t \times((-x) + y)) =(1-t)x+ty. $$

Matrix-vector multiplication in hyperbolic space

A manifold $\mathcal M$ of dimension n is a sort of n-dimensional surface. At each point $x\in\mathcal M$, we can define its tangent space $T_x\mathcal M$, an n-dimensional vector space, which is a local, first order approximation of the manifold around $x$.

Then, if you take a vector $v$, tangent to $\mathcal M$ at $x$, and want to move inside the manifold in the direction of $v$, you have to use a map called the exponential map at $x$: $$ \exp_{x} : T_{x} \mathcal{M} \rightarrow \mathcal{M}. $$ Now the log map is just its inverse: $$\log_x\ :\quad\mathcal{M}\to T_x\mathcal M.$$ We get the following formula:

$$r\otimes x = \exp_0(r\log_0(x)).$$ This means that the Möbius scalar multiplication of x by r corresponds to

  • Moving $x$ to the tangent space at $0$ of the Poincaré ball using $\log_0$,
  • Multiplying this vector by $r$, since $\log_0(x)$ is now in the vector space $T_x\mathbb{D}^n=\mathbb{R}^n$,
  • Projecting it back on the manifold using the exp map at $0$.

We propose to define matrix-vector multiplications in the Poincaré ball in a similar manner:

$$M\otimes x\ := \exp_0(M\log_0(x)).$$

$$M^{\otimes} \mathbf{x} =\frac{1}{\sqrt{c}} \tanh \left(\frac{|M \mathbf{x}|}{|x|} \operatorname{arctanh}(\sqrt{c}|\mathbf{x}|)\right) \frac{M \mathbf{x}}{|M \mathbf{x}|} $$

  • Matrix associativity: $M\otimes (N\otimes x)\ = (MN)\otimes x$
  • Compatibility with scalar multiplication: $M\otimes (r\otimes x)\ = (rM)\otimes x = r\otimes(M\otimes x)$
  • Directions are preserved: $M\otimes x/\parallel M\otimes x\parallel = Mx/\parallel Mx\parallel$ for $Mx\neq 0$
  • Rotations are preserved: $M\otimes x= Mx$ for $M\in\mathcal{O}_n(\mathbb{R})$

Hyperbolic softmax

In order to generalize multinomial logistic regression (MLR, also called softmax regression), we proceed in 3 steps:

We first reformulate softmax probabilities with a distance to a margin hyperplane Second, we define hyperbolic hyperplanes Finally, by finding the closed-form formula of the distance between a point and a hyperbolic hyperplane, we derive the final formula.

Similarly as for the hyperbolic GRU, we show that when the Poincaré ball in continuously flattened to Euclidean space (sending its radius to infinity), hyperbolic softmax converges to Euclidean softmax.

Hyperbolic RNN

A natural adaptation of RNN using our formulas yields:

$$h_{t+1} = \varphi^{\otimes}\left(((W\otimes h_t)\oplus(U\otimes x_t))\oplus b\right).$$

hGRU

$$ \begin{array}{l}{r_{t}=\sigma \log_{0}\left(\left(\left(W^{r} \otimes h_{t-1}\right) \oplus\left(U^{r} \otimes x_{t}\right)\right) \oplus b^{r}\right)} \ { z_{t}=\sigma \log_{0}\left(\left(\left(W^{z} \otimes h_{t-1}\right) \oplus\left(U^{z} \otimes x_{t}\right)\right) \oplus b^{z}\right)} \ {\left.\tilde{h}{t}=\varphi^{\otimes}\left(\left(\left(W \operatorname{diag}\left(r{t}\right)\right] \otimes h_{t-1}\right) \oplus\left(U \otimes x_{t}\right)\right) \oplus b\right)} \ {h_{t}=h_{t-1} \oplus\left(\operatorname{diag}\left(z_{t}\right) \otimes\left(\left(-h_{t-1}\right) \oplus \widetilde{h_{t}}\right)\right)}\end{array} $$

Hyperbolic Attention Networks

Recent approaches have successfully demonstrated the benefits of learning the parameters of shallow networks in hyperbolic space. We extend this line of work by imposing hyperbolic geometry on the embeddings used to compute the ubiquitous attention mechanisms for different neural networks architectures. By only changing the geometry of embedding of object representations, we can use the embedding space more efficiently without increasing the number of parameters of the model. Mainly as the number of objects grows exponentially for any semantic distance from the query, hyperbolic geometry --as opposed to Euclidean geometry-- can encode those objects without having any interference. Our method shows improvements in generalization on neural machine translation on WMT'14 (English to German), learning on graphs (both on synthetic and real-world graph tasks) and visual question answering (CLEVR) tasks while keeping the neural representations compact.

Hyperbolic Recommender Systems

Graph Convolutional Network

If images is regarded as a matrix in computer and text as a chain( or sequence), their representation contain all the spatial and semantic information of the entity.

Graph can be represented as adjacency matrix as shown in Graph Algorithm. However, the adjacency matrix only describe the connections between the nodes. The feature of the nodes does not appear. The node itself really matters. For example, the chemical bonds can be represented as adjacency matrix while the atoms in molecule really determine the properties of the molecule.

A simple and direct way is to concatenate the feature matrix $X\in \mathbb{R}^{N\times E}$ and adjacency matrix $A\in\mathbb{B}^{N\times N}$, i.e., $X_{in}=[X, A]\in \mathbb{R}^{N\times (N+E)}$. What is more, $\mathbb{B}$ is binary where each element of the adjacent matrix $a_{i,j}$ is ${1}$ if the node ${i}$ is adjacent to the node ${j}$ otherwise 0.

And what is the output? How can deep learning apply to them? And how can we extend the tree-based algorithms such as decision tree into graph-based algorithms?

For these models, the goal is then to learn a function of signals/features on a graph $G=(V,E)$ which takes as input:

  • A feature description $x_i$ for every node $i$; summarized in a $N\times D$ feature matrix ${X}$ ($N$: number of nodes, $D$: number of input features);
  • A representative description of the graph structure in matrix form; typically in the form of an adjacency matrix ${A}$ (or some function thereof)

and produces a node-level output $Z$ (an $N\times F$ feature matrix, where $F$ is the number of output features per node). Graph-level outputs can be modeled by introducing some form of pooling operation (see, e.g. Duvenaud et al., NIPS 2015).

Every neural network layer can then be written as a non-linear function $$ {H}{i+1} = \sigma \circ ({H}{i}, A) $$ with ${H}0 = {X}{in}$ and ${H}_{d} = Z$ (or $Z$ for graph-level outputs), $d$ being the number of layers. The specific models then differ only in how $\sigma$ is chosen and parameterized.

For example, we can consider a simple form of a layer-wise propagation rule $$ {H}{i+1} = \sigma \circ ({H}{i}, A)=\sigma \circ(A {H}{i} {W}{i}) $$ where ${W}_{i}$ is a weight matrix for the $i$-th neural network layer and $\sigma (\cdot)$ is is a non-linear activation function such as ReLU.

  • But first, let us address two limitations of this simple model: multiplication with $A$ means that, for every node, we sum up all the feature vectors of all neighboring nodes but not the node itself (unless there are self-loops in the graph). We can "fix" this by enforcing self-loops in the graph: we simply add the identity matrix $I$ to $A$.

  • The second major limitation is that $A$ is typically not normalized and therefore the multiplication with $A$ will completely change the scale of the feature vectors (we can understand that by looking at the eigenvalues of $A$).Normalizing ${A}$ such that all rows sum to one, i.e. $D^{-1}A$, where $D$ is the diagonal node degree matrix, gets rid of this problem.

In fact, the propagation rule introduced in Kipf & Welling (ICLR 2017) is given by: $$ {H}{i+1} = \sigma \circ ({H}{i}, A)=\sigma \circ(\hat{D}^{-\frac{1}{2}} \hat{A} \hat{D}^{-\frac{1}{2}} {H}{i} {W}{i}), $$ with $\hat{A}=A+I$, where $I$ is the identity matrix and $\hat{D}$ is the diagonal node degree matrix of $\hat{A}$. See more details at Multi-layer Graph Convolutional Networks (GCN) with first-order filters.

Like other neural network, GCN is also composite of linear and nonlinear mapping. In details,

  1. $\hat{D}^{-\frac{1}{2}} \hat{A} \hat{D}^{-\frac{1}{2}}$ is to normalize the graph structure;
  2. the next step is to multiply node properties and weights;
  3. Add nonlinearities by activation function $\sigma$.

See more at experoinc.com or https://tkipf.github.io/.

That seems simple enough, but many graphs, like social network graphs with billions of nodes (where each member is a node and each connection to another member is an edge), are simply too large to be computed. Size is one problem that graphs present as a data structure. In other words, you can’t efficiently store a large social network in a tensor. They don’t compute.

Neural nets do well on vectors and tensors; data types like images (which have structure embedded in them via pixel proximity – they have fixed size and spatiality); and sequences such as text and time series (which display structure in one direction, forward in time).

Graphs have an arbitrary structure: they are collections of things without a location in space, or with an arbitrary location. They have no proper beginning and no end, and two nodes connected to each other are not necessarily “close”.

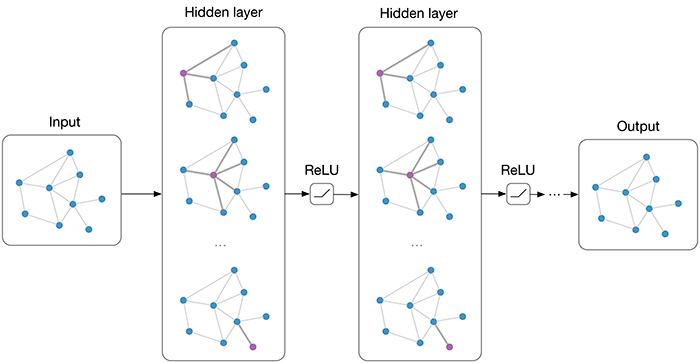
$\color{navy}{\text{Graph convolution network is potential to}}, \mathcal{reasoning}$ as the blend of $\frak{\text{probabilistic graph model}}$ and $\mathcal{\text{deep learning}}$.

GCN can be regarded as the counterpart of CNN for graphs so that the optimization techniques such as normalization, attention mechanism and even the adversarial version can be extended to the graph structure.

Spectral ConvNets

Compositional layers of convolutional neural network can be expressed as

$$ \hat{H}{i} = P\oplus H{i-1} \ \tilde{H_i} = C_i\otimes(\hat{H}_{t}) \ Z_i = \mathrm{N}\cdot \tilde{H_i} \ H_i = Pooling\cdot (\sigma\circ Z_i) $$

where $\otimes,\oplus,\cdot$ represent convolution operation, padding and pooling, respectively.

Xavier Bresson gave a talk on New Deep Learning Techniques FEBRUARY 5-9, 2018. We would ideally like our graph convolutional layer to have:

  • Computational and storage efficiency (requiring no more than $O(E+V)$ time and memory);
  • Fixed number of parameters (independent of input graph size);
  • Localisation (acting on a local neighbourhood of a node);
  • Ability to specify arbitrary importances to different neighbours;
  • Applicability to inductive problems (arbitrary, unseen graph structures).
CNN GCN ---
padding ? ?
convolution ? Information of neighbors
pooling ? Invariance
  • Spectral graph theory allows to redefine convolution in the context of graphs with Fourier analysis.
  • Graph downsampling $\iff$ graph coarsening $\iff$ graph partitioning: Decompose ${G}$ into smaller meaningful clusters.
  • Structured pooling: Arrangement of the node indexing such that adjacent nodes are hierarchically merged at the next coarser level.

Laplacian operator is represented as a positive semi-definite $n \times n$ matrix:

Laplacian Representation
Unnormalized Laplacian $\Delta = \bf{D - A}$
Normalized Laplacian $\Delta = \bf{I -D^{-\frac{1}{2}}AD^{-\frac{1}{2}}}$
Random walk Laplacian $\Delta = \bf{I - D^{-1}A}$
$\mathbf A$：Adjacency Matrix $\mathbf D$: Degree Matrix

Eigendecomposition of graph Laplacian:

$$\Delta = {\Phi}^{T} {\Lambda} {\Phi}$$

where ${\Phi}$ is the matrix consisting of eigenvectors and ${\Lambda}= diag({\lambda}_1，\dots, {\lambda}n )$. In matrix-vector notation, with the $n\times n$ Fourier matrix and a n-dimensional vector $f\in\mathbb{R}^{n}$, it is proven that if $\hat{f}={\Phi}^{T}f$ as the projection of $f$ into the column space of $\Phi$, where $\hat{f}{i}$ the inner product of ${f, \phi_i}$, then $f={\Phi}\hat{f}$ the inverse Fourier transform.

Convolution of two vectors $f=(f_1, \cdots, f_n )^{T}$ and $g=(g_1, \cdots, g_n )^{T}$ is defined as $(f\star g)i = \sum{m} g_{(i-m) ,,, mod ,,,n } ,\cdot f_m$ or in matrix notation $$ (f\star g)= \underbrace{\begin{pmatrix} & g_1, & g_2, & \cdots, & g_{n-1}, & g_n &\ & g_n, & g_1, & \cdots, & g_{n-2}, & g_{n-1} & \ & \vdots & \vdots &\ddots & \vdots & \vdots & \ & g_3, & g_4, & \cdots, & g_{1}, & g_2 &\ & g_2, & g_3, & \cdots, & g_{n}, & g_1 &\ \end{pmatrix}}_{\text{Circulant matrix G} } \begin{pmatrix} f_1 \ \vdots \ f_n \end{pmatrix} \ = \underbrace{ {\Phi} {diag(\hat{g}_1, \cdots, \hat{g}m)} \Phi^T }{G} \quad f \ = {\Phi}({\Phi}^Tg\circ {\Phi}^{T} f) $$

where the last equation is because the matrix multiplication is associative and $\Phi^Tg$ is the $\fbox{Fourier transform}$; the notation $\circ$ is the inner product. What is more, $${\Phi}({\Phi}^Tg\circ {\Phi}^{T} f)={\Phi}\hat{g}(\Lambda){\Phi}^{T} f=\hat{g}({\Phi}(\Lambda){\Phi}^{T})f=\hat{g}(\Delta)f$$ where $\Delta$ is the Laplacian of the graph; $\hat{g}(\Lambda)$ is the polynomial of matrix.

The spectral definition of a convolution-like operation on a non-Euclidean domain allows to parametrize the action of a filter as $$\mathcal{W} \mathbb{f} = \mathbb{\Phi} \hat{\mathbb{W}} \mathbb{\Phi}^{T}\mathbb{f},$$

where $\hat{\mathbb{W}}$ is a diagonal weight matrix containing the filter’s frequency response on the diagonal. In the space domain, it amounts to applying the operator $\mathcal W = \mathbb{\Phi} \hat{\mathbb{W}} \mathbb{\Phi}^{T}$ to $\mathbb f$ by computing the inner products of $\mathbb{f}$ with every row of $\mathcal{W}$ and stacking the resulting numbers into a vertex field. Different weight matrices $\hat{\mathbb W}$ realize different such operators.

To mimick the construction of a regular CNN, we construct a spectral convolutional layer accepting an m-dimensional vertex field $x=(x^1,\dots,x^m)$ and outputting an m′-dimensional vertex field $y=(y^1,\dots,y^{m′})$, whose i-the dimension is defined according to $$\mathbb{y}j = \varphi\left( \sum{i=1}^m \mathbb{\Phi} \hat{\mathbb{W}}^{ij} \mathbb{\Phi}^{T} \mathbb{x}^i \right),$$ where $\varphi$ is an element-wise non-linearity such as ReLU, and $\hat{\mathbb{W}}^{ij}$, are diagonal matrices parametrizing the filters of the layer.

Graph Convolution: Recursive Computation with Shared Parameters:

  • Represent each node based on its neighborhood
  • Recursively compute the state of each node by propagating previous states using relation specific transformations
  • Backpropagation through Structure

We would like to impose spatial localization onto the weights $\hat{\mathbb{W}}^{ij}$, that is, ensure that the vertex fields defined by every row of the operator ${W} = {\Phi} \hat{{W}} {\Phi}^{T}$ are spatially localized.

Vanilla spectral graph ConvNets

Every graph convolutional layer starts off with a shared node-wise feature transformation (in order to achieve a higher-level representation), specified by a weight matrix $W$. This transforms the feature vectors into $\vec{g}_i = {\bf W}\vec{h}_i$. After this, the vectors $\vec{g}_i$ are typically recombined in some way at each node.

In general, to satisfy the localization property, we will define a graph convolutional operator as an aggregation of features across neighborhoods; defining $\mathcal{N}_i$ as the neighborhood of node i (typically consisting of all first-order neighbors of $i$ , including $i$ itself), we can define the output features of node $i$ as: $$\vec{h}i' = \sigma\left(\sum{j\in\mathcal{N}i}\alpha{ij}\vec{g}_j\right)$$ where $\sigma$ is some activation function such as rectified linear unit (ReLU) in ConvNet.

SplineNets

Parametrize the smooth spectral filter function

Spectral graph ConvNets with polynomial filters

Represent smooth spectral functions with polynomials of Laplacian eigenvalues $$w_{\alpha}(\lambda)={\sum}{j=0}^r{\alpha}{j} {\lambda}^j$$

where $\alpha=(\alpha_1, \cdots, \alpha_r)^{T}$ is the vector of filter parameters

Convolutional layer: Apply spectral filter to feature signal ${f}$: $$w_{\alpha}(\Lambda)f= {\sum}{j=0}^r{\alpha}{j} {\Lambda}^j f$$

Such graph convolutional layers are GPU friendly.

ChebNet

Graph convolution network always deal with unstructured data sets where the graph has different size. What is more, the graph is dynamic, and we need to apply to new nodes without model retraining.

Graph convolution with (non-orthogonal) monomial basis $1, x, x^2, x^3, \cdots$: $$w_{\alpha}(\lambda)={\sum}{j=0}^{r}{\alpha}{j} {\lambda}^{j}$$ Graph convolution with (orthogonal) Chebyshev polynomials $$w_{\alpha}(\lambda) = {\sum}{j=0}^{r}{\alpha}{j} T_j(\lambda)$$ where $T_k(x)$ are the Chebyshev polynomials.

Kipf and Welling proposed the ChebNet (arXiv:1609.02907) to approximate the filter using Chebyshev polynomial. Application of the filter with the scaled Laplacian: $$\tilde{\mathbf{\Delta}}=2{\lambda}_{n}^{-1}\mathbf{\Delta-I}$$

$$w_{\alpha}(\tilde{\mathbf{\Delta}})f= {\sum}{j=0}^r{\alpha}{j} T_j({\tilde{\mathbf{\Delta}}}) f={\sum}{j=0}^r{\alpha}{j}X^{(j)}$$ with $$X^{(j)}=T_j({\tilde{\mathbf{\Delta}}}) f=2\mathbf{\Delta} X^{(j-1)}-X^{(j-2)}, X^{(0)}=f, X^{(1)}=\tilde{\mathbf{\Delta}} f.$$

Simplified ChebNets

Use Chebychev polynomials of degree $r=2$ and assume $r_2\approx 2$: $$w_{\alpha}(\tilde{\mathbf{\Delta}})f ={\alpha}_0 f + {\alpha}_1(\mathbf{\Delta-I})f= {\alpha}_0 f - {\alpha}_1\mathbf D^{-\frac{1}{2}}WD^{-\frac{1}{2}} f $$

Further constrain $\alpha=-\alpha_1=\alpha_0$ to obtain a single-parameter filter: $$w_{\alpha}(\tilde{\mathbf{\Delta}})f ={\alpha}\mathbf{(I-D^{-\frac{1}{2}}WD^{-\frac{1}{2}})} f $$

PinSage

ChebNet, CayleyNet, MotifNet

In the previous post, the convolution of the graph Laplacian is defined in its graph Fourier space as outlined in the paper of Bruna et. al. (arXiv:1312.6203). However, the eigenmodes of the graph Laplacian are not ideal because it makes the bases to be graph-dependent. A lot of works were done in order to solve this problem, with the help of various special functions to express the filter functions. Examples include Chebyshev polynomials and Cayley transform.

Graph Convolution Networks (GCNs) generalize the operation of convolution from traditional data (images or grids) to graph data. The key is to learn a function f to generate a node $v_i$’s representation by aggregating its own features $X_i$ and neighbors? features $X_j$ , where $j \in N(v_i)$.

CayleyNet

Defining filters as polynomials applied over the eigenvalues of the graph Laplacian, it is possible indeed to avoid any eigen-decomposition and realize convolution by means of efficient sparse routines The main idea behind CayleyNet is to achieve some sort of spectral zoom property by means of Cayley transform: $$ C(\lambda) = \frac{\lambda - i}{\lambda + i} $$

Instead of Chebyshev polynomials, it approximates the filter as: $$ g(\lambda) = c_0 + \sum_{j=1}^{r}[c_jC^{j}(h\lambda) + c_j^{\ast} C^{j^{\ast}}(h\lambda)] $$ where $c_0$ is real and other $c_j'$ s are generally complex, and ${h}$ is a zoom parameter, and $\lambda'$ s are the eigenvalues of the graph Laplacian. Tuning ${h}$ makes one find the best zoom that spread the top eigenvalues. ${c}$'s are computed by training. This solves the problem of unfavorable clusters in ChebNet.

MotifNet

MotifNet is aimed to address the directed graph convolution.

Minimal inner structures:

  • Invariant by vertex re-indexing (no graph matching is required)
  • Locality (only neighbors are considered) Weight sharing (convolutional operations)
  • Independence w.r.t. graph size

$$\color{green}{\fbox{${h_i} = f_{GCN}(h_j: j\to i)$} }$$

Higher-order Graph Convolutional Networks

Graph Attention Networks

Graph convolutional layer then computes a set of new node features, $(\vec{h}{1},\cdots, \vec{h}{n})$ , based on the input features as well as the graph structure.

Most prior work defines the kernels $\alpha_{ij}$ explicitly (either based on the structural properties of the graph, or as a learnable weight); this requires compromising at least one other desirable property.

In Graph Attention Networks the kernels $\alpha_{ij}$ be computed as a byproduct of an attentional mechanism, $a : \mathbb{R}^N \times \mathbb{R}^N \rightarrow \mathbb{R}$, which computes un-normalized coefficients $e_{ij}$ across pairs of nodes $i,j$ based on their features:

$$ e_{ij} = a(\vec{h}_i, \vec{h}_j). $$

We inject the graph structure by only allowing node $i$ to attend over nodes in its neighbourhood, $j\in\mathcal{N}{i}$.These coefficients are then typically normalised using the softmax function, in order to be comparable across different neighbourhoods: $$ \alpha{ij} = \frac{\exp(e_{ij})}{\sum_{k\in\mathcal{N}i}\exp(e{ik})}. $$

Gated Graph Neural Networks

Generative Models for Graphs

Bayesian GCN

Bayesian-GCNN views the observed graph as a realization from a parametric family of random graphs. We then target inference of the joint posterior of the random graph parameters and the node (or graph) labels using Bayes' theorem. We use a Monte Carlo approximation to achieve this process. In this approximation, three steps of sampling process are involved. First, V samples λv are drawn from the posterior of a family of graph generative model, as shown in Figure 2 (the precise method for generating these samples from the posterior varies depending on the nature of the graph model). Secondly, the NG number of graphs are sampled from the graph generative model using the adopted random graph model, as shown in Figure 3. Thirdly, S weight matrices are sampled from the Bayesian GCNNs using the dropout approximation [4], as shown in Figure 4. The final prediction result is an average of all the predictions coming from different samples, as shown in Figure 5. Comparing to previous graph convolutional neural networks (GCNNs), the main difference is that when we do node label prediction, we will simultaneously learn a graph generation model based on the observed underlying topology, and we learn the parameters of this graph generation model. We can sample a number of similar distributions but diverse topology based on the posterior of the graph generation model. Thus, in the aggregation step of the GCNNs, we are able to learn more general node embedding by incorporating information from different potential neighbors.

Application

GCN for RecSys

PinSAGE Node’s neighborhood defines a computation graph. The key idea is to generate node embeddings based on local neighborhoods. Nodes aggregate information from their neighbors using neural networks.

GCN for Bio & Chem

GCN for NLP

Resource on Geometric Learning