diff --git a/docs/src/lecture_12/LV_GaussNum.svg b/docs/src/lecture_12/LV_GaussNum.svg new file mode 100644 index 00000000..26fa7847 --- /dev/null +++ b/docs/src/lecture_12/LV_GaussNum.svg @@ -0,0 +1,466 @@ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + diff --git a/docs/src/lecture_12/LV_GaussNum2.svg b/docs/src/lecture_12/LV_GaussNum2.svg new file mode 100644 index 00000000..498d80a6 --- /dev/null +++ b/docs/src/lecture_12/LV_GaussNum2.svg @@ -0,0 +1,454 @@ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + diff --git a/docs/src/lecture_12/LV_Measurements.svg b/docs/src/lecture_12/LV_Measurements.svg new file mode 100644 index 00000000..9a879a44 --- /dev/null +++ b/docs/src/lecture_12/LV_Measurements.svg @@ -0,0 +1,454 @@ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + diff --git a/docs/src/lecture_12/LV_Measurements2.svg b/docs/src/lecture_12/LV_Measurements2.svg new file mode 100644 index 00000000..0928aeee --- /dev/null +++ b/docs/src/lecture_12/LV_Measurements2.svg @@ -0,0 +1,454 @@ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + diff --git a/docs/src/lecture_12/LV_Quadrics.svg b/docs/src/lecture_12/LV_Quadrics.svg new file mode 100644 index 00000000..1d009506 --- /dev/null +++ b/docs/src/lecture_12/LV_Quadrics.svg @@ -0,0 +1,460 @@ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + diff --git a/docs/src/lecture_12/LV_ensemble.svg b/docs/src/lecture_12/LV_ensemble.svg new file mode 100644 index 00000000..8493de37 --- /dev/null +++ b/docs/src/lecture_12/LV_ensemble.svg @@ -0,0 +1,2368 @@ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + diff --git a/docs/src/lecture_12/cubature.png b/docs/src/lecture_12/cubature.png new file mode 100644 index 00000000..b1793dcb Binary files /dev/null and b/docs/src/lecture_12/cubature.png differ diff --git a/docs/src/lecture_12/euler.jpg b/docs/src/lecture_12/euler.jpg new file mode 100644 index 00000000..0c20ec1f Binary files /dev/null and b/docs/src/lecture_12/euler.jpg differ diff --git a/docs/src/lecture_12/hw.md b/docs/src/lecture_12/hw.md new file mode 100644 index 00000000..3be05358 --- /dev/null +++ b/docs/src/lecture_12/hw.md @@ -0,0 +1,134 @@ +# [Homework 12 - The Runge-Kutta ODE Solver](@id hw12) + +There exist many different ODE solvers. To demonstrate how we can get +significantly better results with a simple update to `Euler`, you will +implement the second order Runge-Kutta method `RK2`: +```math +\begin{align*} +\tilde x_{n+1} &= x_n + hf(x_n, t_n)\\ + x_{n+1} &= x_n + \frac{h}{2}(f(x_n,t_n)+f(\tilde x_{n+1},t_{n+1})) +\end{align*} +``` +`RK2` is a 2nd order method. It uses not only $f$ (the slope at a given point), +but also $f'$ (the derivative of the slope). With some clever manipulations you +can arrive at the equations above with make use of $f'$ without needing an +explicit expression for it (if you want to know how, see +[here](https://web.mit.edu/10.001/Web/Course_Notes/Differential_Equations_Notes/node5.html)). +Essentially, `RK2` computes an initial guess $\tilde x_{n+1}$ to then average +the slopes at the current point $x_n$ and at the guess $\tilde x_{n+1}$ which +is illustarted below. +![rk2](rk2.png) + +The code from the lab that you will need for this homework is given below. +As always, put all your code in a file called `hw.jl`, zip it, and upload it +to BRUTE. +```@example hw +struct ODEProblem{F,T<:Tuple{Number,Number},U<:AbstractVector,P<:AbstractVector} + f::F + tspan::T + u0::U + θ::P +end + + +abstract type ODESolver end + +struct Euler{T} <: ODESolver + dt::T +end + +function (solver::Euler)(prob::ODEProblem, u, t) + f, θ, dt = prob.f, prob.θ, solver.dt + (u + dt*f(u,θ), t+dt) +end + + +function solve(prob::ODEProblem, solver::ODESolver) + t = prob.tspan[1]; u = prob.u0 + us = [u]; ts = [t] + while t < prob.tspan[2] + (u,t) = solver(prob, u, t) + push!(us,u) + push!(ts,t) + end + ts, reduce(hcat,us) +end + + +# Define & Solve ODE + +function lotkavolterra(x,θ) + α, β, γ, δ = θ + x₁, x₂ = x + + dx₁ = α*x₁ - β*x₁*x₂ + dx₂ = δ*x₁*x₂ - γ*x₂ + + [dx₁, dx₂] +end +``` +```@raw html +
+
Homework (2 points)
+
+``` +Implement the 2nd order Runge-Kutta solver according to the equations given above +by overloading the call method of a new type `RK2`. +```julia +(solver::RK2)(prob::ODEProblem, u, t) +``` +```@raw html +
+``` + +```@setup hw +struct RK2{T} <: ODESolver + dt::T +end +function (solver::RK2)(prob::ODEProblem, u, t) + f, θ, dt = prob.f, prob.θ, solver.dt + du = f(u,θ) + uh = u + du*dt + u + dt/2*(du + f(uh,θ)), t+dt +end +``` +You should be able to use it exactly like our `Euler` solver before: +```@example hw +using Plots +using JLD2 + +# Define ODE +function lotkavolterra(x,θ) + α, β, γ, δ = θ + x₁, x₂ = x + + dx₁ = α*x₁ - β*x₁*x₂ + dx₂ = δ*x₁*x₂ - γ*x₂ + + [dx₁, dx₂] +end + +θ = [0.1,0.2,0.3,0.2] +u0 = [1.0,1.0] +tspan = (0.,100.) +prob = ODEProblem(lotkavolterra,tspan,u0,θ) + +# load correct data +true_data = load("lotkadata.jld2") + +# create plot +p1 = plot(true_data["t"], true_data["u"][1,:], lw=4, ls=:dash, alpha=0.7, + color=:gray, label="x Truth") +plot!(p1, true_data["t"], true_data["u"][2,:], lw=4, ls=:dash, alpha=0.7, + color=:gray, label="y Truth") + +# Euler solve +(t,X) = solve(prob, Euler(0.2)) +plot!(p1,t,X[1,:], color=3, lw=3, alpha=0.8, label="x Euler", ls=:dot) +plot!(p1,t,X[2,:], color=4, lw=3, alpha=0.8, label="y Euler", ls=:dot) + +# RK2 solve +(t,X) = solve(prob, RK2(0.2)) +plot!(p1,t,X[1,:], color=1, lw=3, alpha=0.8, label="x RK2") +plot!(p1,t,X[2,:], color=2, lw=3, alpha=0.8, label="y RK2") +``` diff --git a/docs/src/lecture_12/lab-ode.jl b/docs/src/lecture_12/lab-ode.jl new file mode 100644 index 00000000..44617a12 --- /dev/null +++ b/docs/src/lecture_12/lab-ode.jl @@ -0,0 +1,49 @@ +struct ODEProblem{F,T<:Tuple{Number,Number},U<:AbstractVector,P<:AbstractVector} + f::F + tspan::T + u0::U + θ::P +end + + +abstract type ODESolver end + +struct Euler{T} <: ODESolver + dt::T +end + +function (solver::Euler)(prob::ODEProblem, u, t) + f, θ, dt = prob.f, prob.θ, solver.dt + (u + dt*f(u,θ), t+dt) +end + + +function solve(prob::ODEProblem, solver::ODESolver) + t = prob.tspan[1]; u = prob.u0 + us = [u]; ts = [t] + while t < prob.tspan[2] + (u,t) = solver(prob, u, t) + push!(us,u) + push!(ts,t) + end + ts, reduce(hcat,us) +end + + +# Define & Solve ODE + +function lotkavolterra(x,θ) + α, β, γ, δ = θ + x₁, x₂ = x + + dx₁ = α*x₁ - β*x₁*x₂ + dx₂ = δ*x₁*x₂ - γ*x₂ + + [dx₁, dx₂] +end + +θ = [0.1,0.2,0.3,0.2] +u0 = [1.0,1.0] +tspan = (0.,100.) +prob = ODEProblem(lotkavolterra,tspan,u0,θ) + diff --git a/docs/src/lecture_12/lab.jl b/docs/src/lecture_12/lab.jl new file mode 100644 index 00000000..43e19056 --- /dev/null +++ b/docs/src/lecture_12/lab.jl @@ -0,0 +1,182 @@ +using Zygote + +struct GaussNum{T<:Real} <: Real + μ::T + σ::T +end +mu(x::GaussNum) = x.μ +sig(x::GaussNum) = x.σ +GaussNum(x,y) = GaussNum(promote(x,y)...) +±(x,y) = GaussNum(x,y) +Base.convert(::Type{T}, x::T) where T<:GaussNum = x +Base.convert(::Type{GaussNum{T}}, x::Number) where T = GaussNum(x,zero(T)) +Base.promote_rule(::Type{GaussNum{T}}, ::Type{S}) where {T,S} = GaussNum{T} +Base.promote_rule(::Type{GaussNum{T}}, ::Type{GaussNum{T}}) where T = GaussNum{T} + +# convert(GaussNum{Float64}, 1.0) |> display +# promote(GaussNum(1.0,1.0), 2.0) |> display +# error() + +#+(x::GaussNum{T},a::T) where T =GaussNum(x.μ+a,x.σ) +#+(a::T,x::GaussNum{T}) where T =GaussNum(x.μ+a,x.σ) +#-(x::GaussNum{T},a::T) where T =GaussNum(x.μ-a,x.σ) +#-(a::T,x::GaussNum{T}) where T =GaussNum(x.μ-a,x.σ) +#*(x::GaussNum{T},a::T) where T =GaussNum(x.μ*a,a*x.σ) +#*(a::T,x::GaussNum{T}) where T =GaussNum(x.μ*a,a*x.σ) + + +# function Base.:*(x1::GaussNum, x2::GaussNum) +# f(x1,x2) = x1 * x2 +# s1 = Zygote.gradient(μ -> f(μ,x2.μ), x1.μ)[1]^2 * x1.σ^2 +# s2 = Zygote.gradient(μ -> f(x1.μ,μ), x2.μ)[1]^2 * x2.σ^2 +# GaussNum(f(x1.μ,x2.μ), sqrt(s1+s2)) +# end + +function _uncertain(f, args::GaussNum...) + μs = [x.μ for x in args] + dfs = Zygote.gradient(f,μs...) + σ = map(zip(dfs,args)) do (df,x) + df^2 * x.σ^2 + end |> sum |> sqrt + GaussNum(f(μs...), σ) +end + +function _uncertain(expr::Expr) + if expr.head == :call + :(_uncertain($(expr.args[1]), $(expr.args[2:end]...))) + else + error("Expression has to be a :call") + end +end + +macro uncertain(expr) + _uncertain(expr) +end + +getmodule(f) = first(methods(f)).module + +function _register(func::Symbol) + mod = getmodule(eval(func)) + :($(mod).$(func)(args::GaussNum...) = _uncertain($func, args...)) +end + +function _register(funcs::Expr) + Expr(:block, map(_register, funcs.args)...) +end + +macro register(funcs) + _register(funcs) +end + +@register - + * + +f(x,y) = x+y*x + + +# @register * +# @register + +# @register - +# @register f + +asdf(x1::GaussNum{T},x2::GaussNum{T}) where T =GaussNum(x1.μ*x2.μ, sqrt((x2.μ*x1.σ).^2 + (x1.μ * x2.σ).^2)) +gggg(x1::GaussNum{T},x2::GaussNum{T}) where T =GaussNum(x1.μ+x2.μ, sqrt(x1.σ.^2 + x2.σ.^2)) + +x1 = GaussNum(rand(),rand()) +x2 = GaussNum(rand(),rand()) + +display(x1*x2) +display(asdf(x1,x2)) +display(_uncertain(*,x1,x2)) +display(@uncertain x1*x2) + +display(x1-x2) +display(x1+x2) +display(f(x1,x2)) +#error() + + +using Plots +using JLD2 + +abstract type AbstractODEProblem end + +struct ODEProblem{F,T,U,P} <: AbstractODEProblem + f::F + tspan::T + u0::U + θ::P +end + +abstract type ODESolver end +struct Euler{T} <: ODESolver + dt::T +end +struct RK2{T} <: ODESolver + dt::T +end + +function f(x,θ) + α, β, γ, δ = θ + x₁, x₂ = x + + dx₁ = α*x₁ - β*x₁*x₂ + dx₂ = δ*x₁*x₂ - γ*x₂ + + [dx₁, dx₂] +end + +function solve(prob::AbstractODEProblem, solver::ODESolver) + t = prob.tspan[1]; u = prob.u0 + us = [u]; ts = [t] + while t < prob.tspan[2] + (u,t) = solver(prob, u, t) + push!(us,u) + push!(ts,t) + end + ts, reduce(hcat,us) +end + +function (solver::Euler)(prob::ODEProblem, u, t) + f, θ, dt = prob.f, prob.θ, solver.dt + (u + dt*f(u,θ), t+dt) +end + +function (solver::RK2)(prob::ODEProblem, u, t) + f, θ, dt = prob.f, prob.θ, solver.dt + uh = u + f(u,θ)*dt + u + dt/2*(f(u,θ) + f(uh,θ)), t+dt +end + + +@recipe function plot(ts::AbstractVector, xs::AbstractVector{<:GaussNum}) + # you can set a default value for an attribute with `-->` + # and force an argument with `:=` + μs = [x.μ for x in xs] + σs = [x.σ for x in xs] + @series begin + :seriestype := :path + # ignore series in legend and color cycling + primary := false + linecolor := nothing + fillcolor := :lightgray + fillalpha := 0.5 + fillrange := μs .- σs + # ensure no markers are shown for the error band + markershape := :none + # return series data + ts, μs .+ σs + end + ts, μs +end + +θ = [0.1,0.2,0.3,0.2] +u0 = [GaussNum(1.0,0.1),GaussNum(1.0,0.1)] +tspan = (0.,100.) +dt = 0.1 +prob = ODEProblem(f,tspan,u0,θ) + +t,X=solve(prob, RK2(0.2)) +p1 = plot(t, X[1,:], label="x", lw=3) +plot!(p1, t, X[2,:], label="y", lw=3) + +display(p1) diff --git a/docs/src/lecture_12/lab.md b/docs/src/lecture_12/lab.md new file mode 100644 index 00000000..c162d12a --- /dev/null +++ b/docs/src/lecture_12/lab.md @@ -0,0 +1,429 @@ +# [Lab 12 - Differential Equations](@id lab12) + +In this lab you will implement a simple solver for *ordinary differential +equations* (ODE) as well as a less verbose version of the `GaussNum`s that were +introduced in the lecture. + +## Euler ODE Solver + +In this first part you will implement your own, simple, ODE framwork (feel free +to make it a package;) in which you can easily specify different ODE solvers. +The API is heavily inspired by [`DifferentialEquations.jl`](https://diffeq.sciml.ai/stable/), +so if you ever need to use it, you will already have a feeling for how it works. + +Like in the lecture, we want to be able to specify an ODE like below. +```@example lab +function lotkavolterra(x,θ) + α, β, γ, δ = θ + x₁, x₂ = x + + dx₁ = α*x₁ - β*x₁*x₂ + dx₂ = δ*x₁*x₂ - γ*x₂ + + [dx₁, dx₂] +end +nothing # hide +``` +In the lecture we then solved it with a `solve` function that received all necessary +arguments to fully specify how the ODE should be solved. The number of necessary arguments +to `solve` can quickly become very large, so we will introduce a new API for `solve` +which will always take only two arguments: `solve(::ODEProblem, ::ODESolver)`. +The `solve` function will only do some book-keeping and call the solver until +the ODE is solved for the full `tspan`. + +The `ODEProblem` will contain all necessary parameters to fully specify the ODE +that should be solved. In our case that is the function `f` that defines the +ODE itself, initial conditions `u0`, ODE parameters `θ`, and the time domain of +the ODE `tspan`: +```@example lab +struct ODEProblem{F,T<:Tuple{Number,Number},U<:AbstractVector,P<:AbstractVector} + f::F + tspan::T + u0::U + θ::P +end +``` + +The solvers will all be subtyping the abstract type `ODESolver`. The `Euler` solver +from the lecture will need one field `dt` which specifies its time step: +```@example lab +abstract type ODESolver end + +struct Euler{T} <: ODESolver + dt::T +end +``` + +```@raw html +
+
Exercise
+
+``` +Overload the call-method of `Euler` +```julia +(solver::Euler)(prob::ODEProblem, u, t) +``` +such that calling the solver with an `ODEProblem` will perform one step of the +Euler solver and return updated ODE varialbes `u1` and the corresponding +timestep `t1`. +```@raw html +
+
+Solution:

+``` +```@example lab +function (solver::Euler)(prob::ODEProblem, u, t) + f, θ, dt = prob.f, prob.θ, solver.dt + (u + dt*f(u,θ), t+dt) +end +``` +```@raw html +

+``` +```@example lab +# define ODEProblem +θ = [0.1,0.2,0.3,0.2] +u0 = [1.0,1.0] +tspan = (0.,100.) +prob = ODEProblem(lotkavolterra,tspan,u0,θ) + +# run one solver step +solver = Euler(0.2) +(u1,t1) = solver(prob,u0,0.) +``` + +```@raw html +
+
Exercise
+
+``` +Implement the function `solve(::ODEProblem,::ODESolver)` which calls the solver +as many times as are necessary to solve the ODE for the full time domain. +`solve` should return a vector of timesteps and a corresponding matrix of +variables. +```@raw html +
+
+Solution:

+``` +```@example lab +function solve(prob::ODEProblem, solver::ODESolver) + t = prob.tspan[1]; u = prob.u0 + us = [u]; ts = [t] + while t < prob.tspan[2] + (u,t) = solver(prob, u, t) + push!(us,u) + push!(ts,t) + end + ts, reduce(hcat,us) +end +nothing # hide +``` +```@raw html +

+``` + +You can load the true solution and compare it in a plot like below. The file +that contains the correct solution is located here: +[`lotkadata.jld2`](https://github.com/JuliaTeachingCTU/Scientific-Programming-in-Julia/blob/master/docs/src/lecture_12/lotkadata.jld2). +```@example lab +using JLD2 +using Plots + +true_data = load("lotkadata.jld2") + +p1 = plot(true_data["t"], true_data["u"][1,:], lw=4, ls=:dash, alpha=0.7, color=:gray, label="x Truth") +plot!(p1, true_data["t"], true_data["u"][2,:], lw=4, ls=:dash, alpha=0.7, color=:gray, label="y Truth") + +(t,X) = solve(prob, Euler(0.2)) + +plot!(p1,t,X[1,:], color=1, lw=3, alpha=0.8, label="x Euler") +plot!(p1,t,X[2,:], color=2, lw=3, alpha=0.8, label="y Euler") +``` +As you can see in the plot above, the Euler method quickly becomes quite +inaccurate because we make a step in the direction of the tangent which inevitably +leads us away from the perfect solution as shown in the plot below. +![euler](euler.jpg) + +In the [homework](@ref hw12) you will implement a Runge-Kutta solver to get a +much better accuracy with the same step size. + + +## Automating `GaussNum`s + +Next you will implement your own uncertainty propagation. In the lecture you +have already seen the new number type that we need for this: +```@example lab +struct GaussNum{T<:Real} <: Real + μ::T + σ::T +end +``` +```@raw html +
+
Exercise (tiny)
+
+``` +Overload the `±` (type: `\pm`) symbol to define `GaussNum`s like this: `2.0 ± 1.0`. +Additionally, overload the `show` function such that `GaussNum`s are printed +with the `±` as well. +```@raw html +
+
+Solution:

+``` +```@example lab +±(x,y) = GaussNum(x,y) +Base.show(io::IO, x::GaussNum) = print(io, "$(x.μ) ± $(x.σ)") +``` +```@raw html +

+``` + +Recall, that for a function $f(\bm x)$ with $N$ inputs, the uncertainty $\sigma_f$ +is defined by +```math +\sigma_f = \sqrt{\sum_{i=1}^N \left( \frac{df}{dx_i}\sigma_i \right)^2} +``` +To make `GaussNum`s work for arithmetic operations we could +manually implement all desired functions as we started doing in the lecture. +With the autodiff package `Zygote` we can automate the generation of these +functions. In the next two exercises you will implement a macro `@register` +that takes a function and defines the corresponding uncertainty propagation +rule according to the equation above. + +```@raw html +
+
Exercise
+
+``` +Implement a helper function `uncertain(f, args::GaussNum...)` which takes a +function `f` and its `args` and returns the resulting `GaussNum` with an +uncertainty defined by the equation above. + +**Hint**: +You can compute the gradient of a function with Zygote, for example: +```@repl lab +using Zygote; +f(x,y) = x*y; +Zygote.gradient(f, 2., 3.) +``` +```@raw html +
+
+Solution:

+``` +```@example lab +function uncertain(f, args::GaussNum...) + μs = [x.μ for x in args] + dfs = Zygote.gradient(f,μs...) + σ = map(zip(dfs,args)) do (df,x) + (df * x.σ)^2 + end |> sum |> sqrt + GaussNum(f(μs...), σ) +end +nothing # hide +``` +```@raw html +

+``` +Now you can propagate uncertainties through any function like this: +```@repl lab +x1 = 2.0 ± 2.0 +x2 = 2.0 ± 2.0 +uncertain(*, x1, x2) +``` +You can verify the correctness of your implementation by comparing to the manual +implementation from the lecture. +```@raw html +
+
Exercise
+
+``` +For convenience, implement the macro `@register` which will define the +uncertainty propagation rule for a given function. E.g. for the function `*` +the macro should generate code like below +```julia +Base.:*(args::GaussNum...) = uncertain(*, args...) +``` +**Hint**: +If you run into trouble with module names of functions you can make use of +```@repl lab +getmodule(f) = first(methods(f)).module +getmodule(*) +``` +```@raw html +
+
+Solution:

+``` +```@example lab +function _register(func::Symbol) + mod = getmodule(eval(func)) + :($(mod).$(func)(args::GaussNum...) = uncertain($func, args...)) +end + +function _register(funcs::Expr) + Expr(:block, map(_register, funcs.args)...) +end + +macro register(funcs) + _register(funcs) +end +nothing # hide +``` +```@raw html +

+``` +Lets register some arithmetic functions and see if they work +```@repl lab +@register * +x1 * x2 +@register - + +x1 + x2 +x1 - x2 +``` + +To finalize the definition of our new `GaussNum` we can define conversion and +promotion rules such that we do not have to define things like +```julia ++(x::GaussNum, y::Real) = ... ++(x::Real, y::GaussNum) = ... +``` +```@raw html +
+
Exercise
+
+``` +Define `convert` and `promote_rule`s such that you can perform arithmetic operations +on `GaussNum`s and other `Real`s. + +**Hint**: +When converting a normal number to a `GaussNum` you can set the standard deviation +to zero. +```@raw html +
+
+Solution:

+``` +```@example lab +Base.convert(::Type{T}, x::T) where T<:GaussNum = x +Base.convert(::Type{GaussNum{T}}, x::Number) where T = GaussNum(x,zero(T)) +Base.promote_rule(::Type{GaussNum{T}}, ::Type{S}) where {T,S} = GaussNum{T} +Base.promote_rule(::Type{GaussNum{T}}, ::Type{GaussNum{T}}) where T = GaussNum{T} +``` +```@raw html +

+``` +You can test if everything works by adding/multiplying floats to `GuassNum`s. +```@repl lab +1.0±1.0 + 2.0 +``` + +### Propagating Uncertainties through ODEs + +```@raw html +
+
Exercise
+
+``` +With our newly defined `GaussNum` we can easily propagate uncertainties through +our ODE solvers without changing a single line of their code. Try it! +```@raw html +
+
+Solution:

+``` +```@example lab +θ = [0.1±0.001, 0.2, 0.3, 0.2] +u0 = [1.0±0.1, 1.0±0.1] +tspan = (0.,100.) +dt = 0.1 +prob = ODEProblem(lotkavolterra,tspan,u0,θ) + +t,X=solve(prob, Euler(0.1)) +``` +```@raw html +

+``` + +```@raw html +
+
Exercise
+
+``` +Create a plot that takes a `Vector{<:GaussNum}` and plots the mean surrounded +by the uncertainty. +```@raw html +
+
+Solution:

+``` +```@repl lab +mu(x::GaussNum) = x.μ +sig(x::GaussNum) = x.σ + +function uncertainplot(t, x::Vector{<:GaussNum}) + p = plot( + t, + mu.(x) .+ sig.(x), + xlabel = "x", + ylabel = "y", + fill = (mu.(x) .- sig.(x), :lightgray, 0.5), + linecolor = nothing, + primary = false, # no legend entry + ) + + # add the data to the plots + plot!(p, t, mu.(X[1,:])) + + return p +end +``` +```@raw html +

+``` +```@repl lab +uncertainplot(t, X[1,:]) +``` +Unfortunately, with this approach, we would have to define things like `uncertainplot!` +by hand. +To make plotting `GaussNum`s more pleasant we can make use of the `@recipe` +macro from `Plots.jl`. It allows to define plot recipes for custom types +(without having to depend on Plots.jl). Additionally, it makes it easiert to +support all the different ways of creating plots (e.g. via `plot` or `plot!`, +and with support for all keyword args) without having to overload tons of +functions manually. If you want to read more about plot recipies in the docs +of [`RecipesBase.jl`](http://juliaplots.org/RecipesBase.jl/stable/). +An example of a recipe for vectors of `GaussNum`s could look like this: +```@example lab +@recipe function plot(ts::AbstractVector, xs::AbstractVector{<:GaussNum}) + # you can set a default value for an attribute with `-->` + # and force an argument with `:=` + μs = [x.μ for x in xs] + σs = [x.σ for x in xs] + @series begin + :seriestype := :path + # ignore series in legend and color cycling + primary := false + linecolor := nothing + fillcolor := :lightgray + fillalpha := 0.5 + fillrange := μs .- σs + # ensure no markers are shown for the error band + markershape := :none + # return series data + ts, μs .+ σs + end + ts, μs +end + +# now we can easily plot multiple things on to of each other +p1 = plot(t, X[1,:], label="x", lw=3) +plot!(p1, t, X[2,:], label="y", lw=3) +``` + +# References + +* [MIT18-330S12: Chapter 5](https://ocw.mit.edu/courses/mathematics/18-330-introduction-to-numerical-analysis-spring-2012/lecture-notes/MIT18_330S12_Chapter5.pdf) +* [RK2 derivation](https://web.mit.edu/10.001/Web/Course_Notes/Differential_Equations_Notes/node5.html) diff --git a/docs/src/lecture_12/lecture.md b/docs/src/lecture_12/lecture.md new file mode 100644 index 00000000..440d58eb --- /dev/null +++ b/docs/src/lecture_12/lecture.md @@ -0,0 +1,335 @@ +# [Uncertainty Propagation in Ordinary Differential Equations](@id lec12) + +Differential equations are commonly used in science to describe many aspects of the physical world, ranging from dynamical systems and curves in space to complex multi-physics phenomena. + +As an example, consider a simple non-linear ordinary differential equation: + +```math +\begin{align} +\dot{x}&=\alpha x-\beta xy,\\\dot{y}&=-\delta y+\gamma xy, +\end{align} +``` + +Which describes behavior of a predator-pray models in continuous times: + - x is the population of prey (sheep), + - y is the population of predator (wolfes) + - derivatives represent instantaneous growth rates of the populations + - ``t`` is the time and ``\alpha, \beta, \gamma, \delta`` are parameters. + +Can be written in vector arguments ``\mathbf{x}=[x,y]``: +```math +\frac{d\mathbf{x}}{dt}=f(\mathbf{x},\theta) +``` +with arbitrary function ``f`` with vector of parameters ``\theta``. + + +The first steps we may want to do with an ODE is to see it's evolution in time. The most simple approach is to discretize the time axis into steps: +``t = [t_1, t_2, t_3, \ldots t_T]`` +and evaluate solution at these points. + +Replacing derivatives by differences: +```math +\dot x \leftarrow \frac{x_t-x_{t-1}}{\Delta t} +``` +we can derive a general scheme (Euler solution): +```math +\mathbf{x}_t = \mathbf{x}_{t-1} + \Delta{}t f(\mathbf{x}_t,\theta) +``` +which can be written genericaly in julia : +```julia + +function f(x,θ) + α,β,γ,δ = θ + x1,x2=x + dx1 = α*x1 - β*x1*x2 + dx2 = δ*x1*x2 - γ*x2 + [dx1,dx2] +end + +function solve(f,x0::AbstractVector,θ,dt,N) + X = hcat([zero(x0) for i=1:N]...) + X[:,1]=x0 + for t=1:N-1 + X[:,t+1]=X[:,t]+dt*f(X[:,t],θ) + end + X +end +``` + + +Is simple and working (with sufficienty small ``dt``): + +![](lotka.svg) + +ODE of this kind is an example of a "complex" simulation code that we may want to use, interact with, modify or incorporate into a more complex scheme. +- we will test how to re-define the elemnetary oeprations using custom types, automatic differnetiation and automatic code generation +- we will redefine the plotting operation to display the new type correctly +- we will use composition to incorporate the ODE into a more complex solver + + +## Uncertainty propagation + +Prediction of the ODE model is valid only if all parameters and all initial conditions are accurate. This is almost never the case. While the number of sheep can be known, the number of wolfes in a forest is more uncertain. The same model holds for predator-prey in insects where the number of individuals can be only estimated. + +Uncertain initial conditions: +- number of predators and prey given by a probability distribution +- interval ``[0.8,1.2]`` corresponds to uniform distribution ``U(0.8,1.2)`` +- gaussian ``N(\mu,\sigma)``, with mean ``\mu`` and standard deviation ``\sigma`` e.g. ``N(1,0.1)`` +- more complicated distributions are more realistic (the number of animals is not negative!) + +### Ensemble approach + +The most simple approach is to represent distribution by an empirical density = discrete samples. +```math +p(\mathbf{x})\approx \frac{1}{K}\sum_{k=1}^{K} \delta(\mathbf{x}-\mathbf{x}^{(k)}) +``` + +In the case of a Gaussian, we just sample: +```julia +K = 10 +X0 = [x0 .+ 0.1*randn(2) for _=1:K] # samples of initial conditions +Xens=[X=solve(f,X0[i],θ0,dt,N) for i=1:K] # solve multiple times +``` +(can be implemented more elegantly using multiple dispatch on Vector{Vector}) + +![](LV_ensemble.svg) + +While it is very simple and universal, it may become hard to interpret. +- What is the probability that it will higher than ``x_{max}``? +- Improving accuracy with higher number of samples (expensive!) + +### Propagating a Gaussian + +Propagation of uncertainty has been studied in many areas of science. Relation between accuracy and computational speed is always a tradeoff. + +A common appoach to propagation of uncertainty is linearized Gaussian: +- variable ``x`` is represented by gaussian ``N(\mu,\sigma)`` +- transformation of addition: ``x+a\sim N(\mu+a,\sigma)`` +- transformation of multiplication: ``a*x\sim N(a*\mu,a*\sigma)`` +- general transformation approximated: +```math +g(x)\sim N(g(\mu),g'(\mu)*\sigma) +``` + +This can be efficienty implemented in Julia: +```julia +struct GNum{T} where T<:Real + μ::T + σ::T +end +import Base: +, * ++(x::GaussNum{T},a::T) where T =GaussNum(x.μ+a,x.σ) ++(a::T,x::GaussNum{T}) where T =GaussNum(x.μ+a,x.σ) +*(x::GaussNum{T},a::T) where T =GaussNum(x.μ*a,a*x.σ) +*(a::T,x::GaussNum{T}) where T =GaussNum(x.μ*a,a*x.σ) +``` + +For the ODE we need multiplication of two Gaussians. Using Taylor expansion and neglecting covariances: +```math +g(x_1,x_2)=N\left(g(\mu_1,\mu_2), \sqrt{\left(\frac{dg}{dx_1}(\mu_1,\mu_2)\sigma_1\right)^2 + \left(\frac{dg}{dx_1}(\mu_1,\mu_2)\sigma_1\right)^2}\right) +``` +which trivially applies to sum: ``x_1+x_2=N(\mu_1+\mu_2, \sqrt{\sigma_1^2 + \sigma_1^2})`` + +```julia ++(x1::GaussNum{T},x2::GaussNum{T}) where T =GaussNum(x1.μ+x2.μ,sqrt(x1.σ.^2 + x2.σ.^2)) +*(x1::GaussNum{T},x2::GaussNum{T}) where T =GaussNum(x1.μ*x2.μ, sqrt(x2.μ*x1.σ.^2 + x1.μ*x2.σ.^2)) + +``` + +Following the principle of defining the necessary functions on the type, we can make it pass through the ODE: +- it is necessary to define new initialization (functions `zero`) +- define nice-looking constructor (``±``) + ```julia + ±(a::T,b::T) where T: can be automated (macro, generated functions) + + +### Flexibility + +The great advantage of the former model was the ability to run an arbitrary code with uncertainty at an arbitrary number. + +For example, we may know the initial conditions, but do not know the parameter value. + +```julia +GX=solve(f,[1.0±0.1,1.0±0.1],[0.1±0.1,0.2,0.3,0.2],0.1,1000) +``` + +![](LV_GaussNum2.svg) + +### Disadvantage + +The result does not correspond to the ensemble version above. +- we have ignored the covariances +- extension to version with covariances is possible by keeping track of the correlations (`Measurements.jl`), where other variables are stored in a dictionary: + - correlations found by language manipulations + - very flexible and easy-to-use + - discovering the covariances requires to build the covariance from `ids`. (Expensive if done too often). + + +## Vector uncertainty +The previous simple approach ignores the covariances between variables. Even if we tract covariances linearnly in the same fashion (``Measurements.jl``), the approach will suffer from a loss of precision under non-linearity. 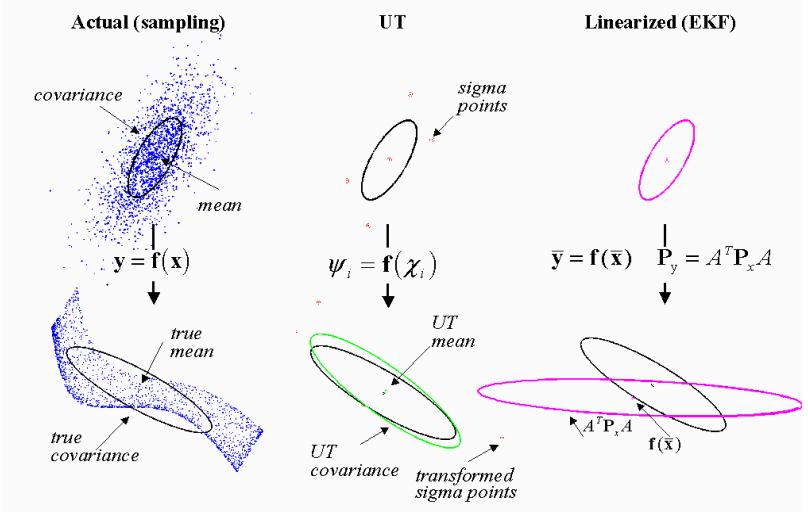+ + +![](https://photos1.blogger.com/blogger/5955/293/1600/unscented-transform-explained.jpg) + +- The linearization-based approach propogates through the non-linearity only the mean and models its neighborhood by a plane. +- Propagating all samples is too expensive +- Methods based on quadrature or cubature rules are a compromise + + +The cubature approach is based on moment matching: +```math +\mu_g = \int g(x) p(x) dx +``` +for which is ``g(\mu)`` poor approximation, corresponding to: +```math +\mu_g = g(\mu) = \int g(x) \delta(x-\mu) dx +``` +For Gaussian distribution, we can use a smarter integration rule, called the Gauss-Hermite quadrature: +```math +\mu_g = \int g(x) p(x) dx \approx \sum_{j=1}^J w_j g(x_j) +``` +where ``x_j`` are prescribed quadrature points (see e.g. ![online tables](https://www.efunda.com/math/num_integration/findgausshermite.cfm)) + +In multivariate setting, the same problem is typically solved with the aim to reduce the computational cost to linear complexity with dimension. Most often aimimg at ``O(2d)`` complexity where ``d`` is the dimension of vector ``x``. + + +One of the most popular approaches today is based on cubature rules approximating the Gaussian in radial-spherical coordinates. + +### Cubature rules + +Consider Gaussian distribution with mean ``\mu`` and covariance matrix ``\Sigma`` that is positive definite with square root ``\sqrt\Sigma``, such that ``\sqrt\Sigma \sqrt\Sigma^T=\Sigma``. The quadrature pints are: +```math +x_i = \mu + \sqrt\Sigma q_i +``` +```math +\begin{align} +q_{1}&=\sqrt{d}\begin{bmatrix}1\\ +0\\ +\vdots +\end{bmatrix} +& +q_{2}&=\sqrt{d}\begin{bmatrix}0\\ +1\\ +\vdots +\end{bmatrix} \ldots +& +q_{d+1}&=\sqrt{d}\begin{bmatrix}-1\\ +0\\ +\vdots +\end{bmatrix} +q_{d+2}&=\sqrt{d}\begin{bmatrix}0\\ +-1\\ +\vdots +\end{bmatrix} \ldots +\end{align} +``` +that can be composed into a matrix ``Q=[q_1,\ldots q_{2d}]`` that is constant: +```math +Q = \sqrt{d} [ I_d, -I_d] +``` + +![](cubature.png) + +Those quadrature points are in integration weighted by: +```math +w_i = \frac{1}{2d}, i=1,\ldots,2d +``` +where ``d`` is dimension of the vectors. + +The quadrature points are propogated through the non-linearity in parallel (``x_i'=g(x_i)``) and the resulting Gaussian distribution is: +```math +\begin{align} +x' & \sim N(\mu',\Sigma')\\ +\mu' & = \frac{1}{2d}\sum_{j=1}^{2d} x'_i\\ +\Sigma &= \frac{1}{2d}\sum_{j=1}^{2d} (x'_i-\mu')^T (x'_i-\mu') +\end{align} +``` + +It is easy to check that if the sigma-points are propagated through an identity, they preserve the mean and variance. +```math +\begin{align} +\mu' & = \frac{1}{2d}\sum_{j=1}^{2d} (\mu + \sqrt{\Sigma}q_i)\\ + & = \frac{1}{2d}(2d\mu + \sqrt{\Sigma} \sum_{j=1}^{2d} (q_i) + & = \mu +\end{align} + +``` + + +For our example: + +![](LV_Quadrics.svg) + +- only 4 trajectories propagated deterministically +- can not be implemented using a single number type + - the number of points to store is proportional to the dimension + - manipulation requires operations from linear algebra +- moving to representations in vector form + - simple for initial conditions, + - how to extend to operate also on parameters? + +### Smarter implementation +Easiest solution is to put the corresponding parts of the problem together: +- ode function ``f``, +- its state ``x0``, +- and parameters ``θ`` +can be wrapped into an ODEProblem + +```julia +struct ODEProblem{F,T,X<:AbstractVector,P<:AbstractVector} + f::F + tspan::T + x0::X + θ::P +end +``` +- the solver can operate on the ODEProbelm type + +### Unceratinty propagation in vectors + +Example: consider uncertainty in state ``[x_1,x_2]`` and the first parameter ``\theta_1``. + +Quick and dirty: +```julia +getuncertainty(o::ODEProblem) = [o.u0[1:2];o.θ[1]] +setuncertainty!(o::ODEProblem,x::AbstractVector) = o.u0[1:2]=x[1:2],o.θ[1]=x[3] +``` +and write a general Cubature solver using multiple dispatch. + +Practical issues: +- how to check bounds? (Asserts) +- what if we provide an incompatible ODEProblem +- define a type that specifies the type of uncertainty? +```julia +struct GaussODEProblem + mean::ODEProblem + unc_in_u # any indexing type accepted by to_index() + unc_in_θ + sqΣ0 +end +``` + +We can dispatch the cubature solver on GaussODEProblem and the ordinary ``solve`` on GaussODEProblem.OP internally. + +```julia +getmean(gop::GaussODEProblem) =[ gop.mean.x0[gop.unc_in_u];gop.mean.θ[gop.unc_in_θ]] +setmean!(gop::GaussODEProblem,x::AbstractVector) = begin + gop.mean.x0[gop.unc_in_u]=x[1:length(gop.unc_in_u)] + gop.mean.θ[gop.unc_in_θ]=x[length(gop.unc_in_u).+[1:length(gop.unc_in_θ)]] +end +``` + +Constructor accepts an ODEProblem with uncertain numbers and converts it to GaussODEProblem: +- goes through ODEProblem ``x0`` and ``θ`` fields and checks their types +- replaces GaussNums in ODEProblem by ordinary numbers +- remembers indices of GaussNum in ``x0`` and ``θ`` +- copies standard deviations in GaussNum to ``sqΣ0`` diff --git a/docs/src/lecture_12/lotka.svg b/docs/src/lecture_12/lotka.svg new file mode 100644 index 00000000..0481fb3d --- /dev/null +++ b/docs/src/lecture_12/lotka.svg @@ -0,0 +1,308 @@ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + diff --git a/docs/src/lecture_12/lotkadata.jl b/docs/src/lecture_12/lotkadata.jl new file mode 100644 index 00000000..1b22a945 --- /dev/null +++ b/docs/src/lecture_12/lotkadata.jl @@ -0,0 +1,25 @@ +using OrdinaryDiffEq +using JLD2 +#using Plots + +function f(x,θ,t) + α,β,γ,δ = θ + x1,x2=x + dx1 = α*x1 - β*x1*x2 + dx2 = δ*x1*x2 - γ*x2 + [dx1,dx2] +end + +θ0 = [0.1,0.2,0.3,0.2] +x0 = [1.0,1.0] +tspan = (0., 100.) +prob = ODEProblem(f,x0,tspan,θ0) +sol = solve(prob,Tsit5()) +#p = plot(sol) + +dt = 0.2 +ts = (tspan[1]):dt:(tspan[2]) +us = reduce(hcat, sol(ts).u) + +data = Dict(:u=>us, :t=>collect(ts)) +jldsave("lotkadata.jld2", u=us, t=collect(ts)) diff --git a/docs/src/lecture_12/lotkadata.jld2 b/docs/src/lecture_12/lotkadata.jld2 new file mode 100644 index 00000000..d6ac297a Binary files /dev/null and b/docs/src/lecture_12/lotkadata.jld2 differ diff --git a/docs/src/lecture_12/ode.jl b/docs/src/lecture_12/ode.jl new file mode 100644 index 00000000..7ca0cf53 --- /dev/null +++ b/docs/src/lecture_12/ode.jl @@ -0,0 +1,151 @@ + +function f(x,θ) + α,β,γ,δ = θ + x1,x2=x + dx1 = α*x1 - β*x1*x2 + dx2 = δ*x1*x2 - γ*x2 + [dx1,dx2] +end + +function solve(f,x0::AbstractVector,θ,dt,N) + X = hcat([zero(x0) for i=1:N]...) + X[:,1]=x0 + for t=1:N-1 + X[:,t+1]=X[:,t]+dt*f(X[:,t],θ) + end + X +end + +θ0 = [0.1,0.2,0.3,0.2] +x0 = [1.0,1.0] +dt = 0.1 +N = 1000 +X=solve(f,x0,θ0,dt,N) + + +using Plots + +p=plot(X[1,:],xlabel="t",label="x",color=:blue) +p=plot!(X[2,:],xlabel="t",label="y",color=:red) + + +K=100 +X0 = [x0 .+ 0.1*randn(2) for k=1:K] +Xens=[X=solve(f,X0[i],θ0,dt,N) for i=1:K] + +for i=1:K + p=plot!(Xens[i][1,:],label="",color=:blue) + p=plot!(Xens[i][2,:],label="",color=:red) +end + +savefig("LV_ensemble.svg") + +using StatsBase +Xm=mean(Xens) +Xstd = std(Xens) + +struct GaussNum{T<:Real} + μ::T + σ::T +end +import Base: +, -, *, zero ++(x::GaussNum{T},a::T) where T =GaussNum(x.μ+a,x.σ) ++(a::T,x::GaussNum{T}) where T =GaussNum(x.μ+a,x.σ) +-(x::GaussNum{T},a::T) where T =GaussNum(x.μ-a,x.σ) +-(a::T,x::GaussNum{T}) where T =GaussNum(x.μ-a,x.σ) +*(x::GaussNum{T},a::T) where T =GaussNum(x.μ*a,a*x.σ) +*(a::T,x::GaussNum{T}) where T =GaussNum(x.μ*a,a*x.σ) + +# TODO +# sin(x::GaussNum)= @uncertain sin(x) + + ++(x1::GaussNum{T},x2::GaussNum{T}) where T =GaussNum(x1.μ+x2.μ, sqrt(x1.σ.^2 + x2.σ.^2)) +-(x1::GaussNum{T},x2::GaussNum{T}) where T =GaussNum(x1.μ-x2.μ, sqrt(x1.σ.^2 + x2.σ.^2)) +*(x1::GaussNum{T},x2::GaussNum{T}) where T =GaussNum(x1.μ*x2.μ, sqrt((x2.μ*x1.σ).^2 + (x1.μ * x2.σ).^2)) +zero(::Type{GaussNum{T}}) where T =GaussNum(zero(T),zero(T)) +zero(x::AbstractVector{T}) where T =[zero(T) for i=1:length(x)] + +function MV(x::AbstractArray{GaussNum{T}}) where T + M=similar(x,T) + V=similar(x,T) + for i=1:length(x) + M[i]=x[i].μ + V[i]=x[i].σ + end + (M,V) +end + +GX=solve(f,[GaussNum(1.0,0.1),GaussNum(1.0,0.1)],[0.1,0.2,0.3,0.2],0.1,1000) +M,V=MV(GX) +plot(M') +plot(M[1,1:30:end],errorbar=V[1,1:30:end],label="x",color=:blue) +plot!(M[2,1:30:end],errorbar=V[2,1:30:end],label="y",color=:red) + +savefig("LV_GaussNum.svg") + +GX=solve(f,[GaussNum(1.0,0.1),GaussNum(1.0,0.1)],[GaussNum(0.1,0.1),0.2,0.3,0.2],0.1,1000) +M,V=MV(GX) +plot(M') +plot(M[1,1:30:end],errorbar=V[1,1:30:end],label="x",color=:blue) +plot!(M[2,1:30:end],errorbar=V[2,1:30:end],label="y",color=:red) + +savefig("LV_GaussNum2.svg") + +using Measurements +MX=solve(f,[1.0±0.1,1.0±0.1],[0.1,0.2,0.3,0.2],0.1,1000) +plot(MX[1,1:30:end],label="x",color=:blue) +plot!(MX[2,1:30:end],label="y",color=:red) + +savefig("LV_Measurements.svg") + +MX=solve(f,[1.0±0.1,1.0±0.1],[0.1±0.01,0.2±0.01,0.3±0.01,0.2±0.01],0.1,1000) +plot(MX[1,1:30:end],label="x",color=:blue) +plot!(MX[2,1:30:end],label="y",color=:red) + +savefig("LV_Measurements2.svg") + + + +# Plot receipe +# plot(Vector{GaussNum}) + +using LinearAlgebra +function solve(f,x0::AbstractVector,sqΣ0, θ,dt,N,Nr) + n = length(x0) + n2 = 2*length(x0) + Qp = sqrt(n)*[I(n) -I(n)] + + X = hcat([zero(x0) for i=1:N]...) + S = hcat([zero(x0) for i=1:N]...) + X[:,1]=x0 + Xp = x0 .+ sqΣ0*Qp + sqΣ = sqΣ0 + Σ = sqΣ* sqΣ' + S[:,1]= diag(Σ) + for t=1:N-1 + if rem(t,Nr)==0 + Xp .= X[:,t] .+ sqΣ * Qp + end + for i=1:n2 # all quadrature points + Xp[:,i].=Xp[:,i] + dt*f(Xp[:,i],θ) + end + mXp=mean(Xp,dims=2) + X[:,t+1]=mXp + Σ=Matrix((Xp.-mXp)*(Xp.-mXp)'/n2) + S[:,t+1]=sqrt.(diag(Σ)) + # @show Σ + + sqΣ = cholesky(Σ).L + + end + X,S +end + +## Extension to arbitrary + +QX,QS=solve(f,[1.0,1.0],(0.1)*I(2),θ0,0.1,1000,1) +plot(QX[1,1:30:end],label="x",color=:blue,errorbar=QS[1,1:30:end]) +plot!(QX[2,1:30:end],label="y",color=:red,errorbar=QS[2,1:30:end]) + +savefig("LV_Quadrics.svg") \ No newline at end of file diff --git a/docs/src/lecture_12/rk2.png b/docs/src/lecture_12/rk2.png new file mode 100644 index 00000000..dc54463a Binary files /dev/null and b/docs/src/lecture_12/rk2.png differ