README.md

PolyhedralFinslerMetrics

---

By : Adam Azlan, Haidan Tang, Melissa George, Yinlan Shao

Goal:

Given a Polyhedral Finsler Metric, write a Python script which can calculate the distance between any two points taken as input, and show a visual representation of this calculation.

So far:

• Created functions for translating between polar/ cartesian coordinates
• Created function for ordering a given set of points based on polar coordinates
• Created function for plotting the shape of a polygon
• Be able to take in points for the polygon from user
• Be able to take in points from user and calculate distance
• Draw a simulation to demonstrate translation/ scaling
  
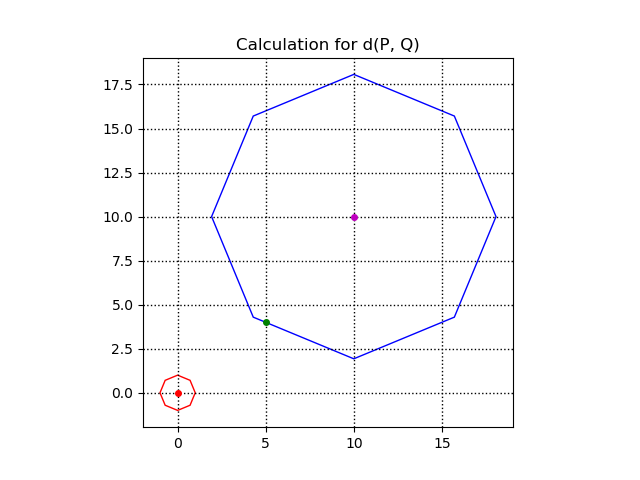
  Given the Polyhedral Finsler Metric defined by a 'unit octagon', the distance between (10, 10) and (5, 4) can be visualized with the following image:
  
  
  
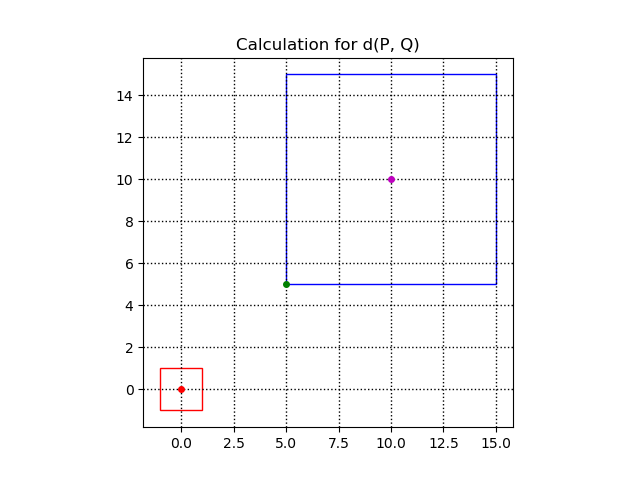
  Given the Polyhedral Finsler Metric defined by a unit square, the distance between (10, 10) and (5, 5) can be visualized with the following image:
  
  
  
  

To do:

• Reduce error with conversions to and from polar coordinates
• Label plots to more clearly show what is happening (Which point is P? Q? What's the scale factor?)
• Create animation that shows the 'translation' and 'scaling' aspects
• Generalize to higher dimensions (3D?)
• Clean up code

Setup:

To be able to run the project yourself, you'll need to do a few things:

• Install Python3
• Install numpy module
• Install matplotlib module

To run:

python3 polyhedral_distance.py

You will be prompted to enter points for the unit polygon. Put in an x value and a y value, separated by a space, and hit enter. Then enter the next point. When finished entering all points, type 'done'. The program will echo your unit polygon back to you.

Please enter a point in the form 'x y' or 'done' to signal you're done entering points:
-1 1
Enter another point or enter 'done':
1 -1
Enter another point or enter 'done':
1 1
Enter another point or enter 'done':
-1 -1
Enter another point or enter 'done':
0 2
Enter another point or enter 'done':
done
The points you entered are:
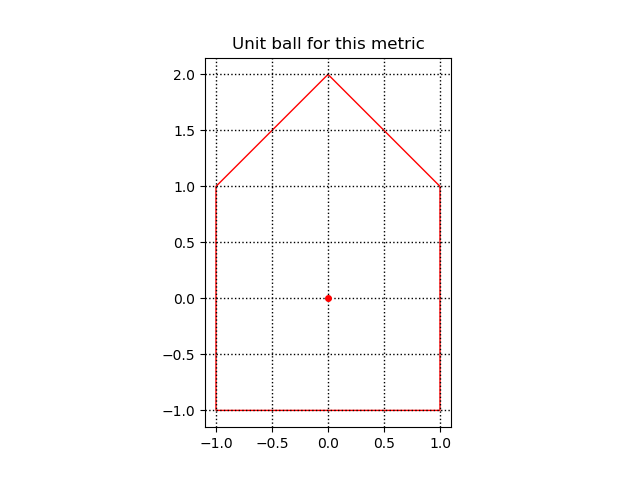
 [(-1.0, 1.0), (1.0, -1.0), (1.0, 1.0), (-1.0, -1.0), (0.0, 2.0)]

After you have defined your metric by entering the points of your unit polygon, a plot of the unit polygon will be displayed. Exit out of this plot to continue.



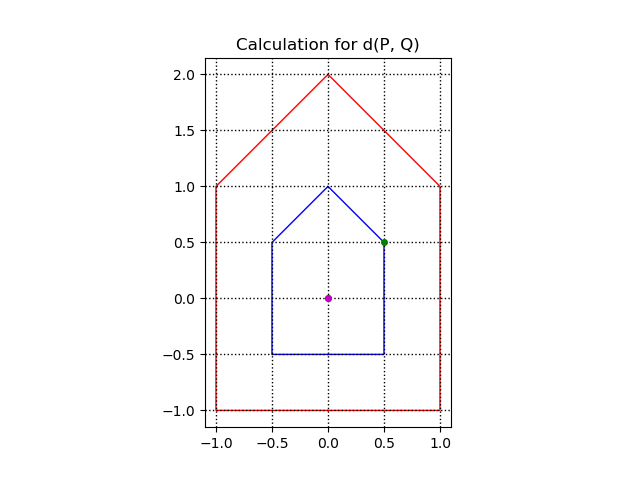
You will now be prompted for points P, Q for which you want to find the distances. Type in the points, and the distance will be displayed, along with an image that shows the translation and scaling that occurred.

You can now start finding distances between points in this metric. Enter points in the form 'x y' when prompted, and type 'quit' at any time.
Enter points P and Q to find the distance between them:
P:0 0
Q:0.5 0.5
Distance between P :  0.0   0.0  and Q :  0.5 0.5  is :  0.5

Continue entering points and calculating distances as long as you wish. Type 'quit' to end the program.