review2015.md

{% include head.html %}

アルゴリズムとデータ構造2015

ハッシュにおける衝突回避方法

ハッシュ法では様々な衝突回避方法が考案されている。

• 連鎖法（チェイン法）
• 開番地法（Open addressing）
• 線形走査法

以下では、格納データ数を $N$、ハッシュ表のサイズを $M$ とする。

連鎖法（チェイン法）

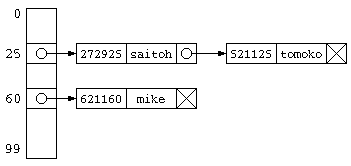
ハッシュテーブルの各番地をリスト構造にし、１つの番地に複数のデータを格納する方法を 連鎖法 という。

• 探索コスト
  • データ件数が少なければ、ハッシュ関数の計算のみでよく、$O(1)$
  • データ件数が多いと、平均長 $N/M$ のリスト探索が必要になり、$O(N)$
• 利点：いくらでもデータを格納できる
• 欠点：データ件数が多いと計算量が $O(N)$ になってしまう

開番地法（オープンアドレス法）

衝突が起きた際に、なんらかの方法で別の空いているアドレスを探す方法を 開番地法 という。ただし、要素の削除で削除記号を残す工夫が必要である（設問２の回答 を参照）。
主要な手法に以下の３つがある。

• 線形走査法
• 二重ハッシュ法
• 均一ハッシュ法

線形走査法（Linear Probing）

衝突が起きるたびに、番地を１つずつずらしていく方法。

１つ目の $h(x)$ を定義した後、ハッシュ関数の列を $$ h_k(x) = h(x) + k \mod M $$ と定義する。衝突が起きた場合は、$h_k(x)$ を順番に試していく。
ただし、再ハッシュのたびに連続した領域を使うため、データが偏った領域に格納される現象 クラスター（clustering）が発生する場合がある。

二重ハッシュ法

衝突が起きるたびに、要素ごとにランダムな大きさ だけずらす¹。 $$ h_k(x) = h(x) + kg(x) \mod M $$

解答（設問２）

衝突を解決する方法として、開番地法の一種である線形操作法を用いる場合、
データの探索アルゴリズム、挿入アルゴリズム、削除アルゴリズムをそれぞれ簡潔に記述せよ。

ハッシュ関数の列を $h_k(x) = h(x)+k \mod m$ とする。
また、挿入・削除・探索を行うデータを $x$ とする。

挿入

$h_1(x), h_2(x),\cdots$ を順番に試していき、空いている番地（または後述の del が格納された番地）が見つかり次第、そこに挿入する。

削除

はじめに $h_1(x), h_2(x),\cdots$ を順番に試していき、$x$ の格納された番地まで移動する。$x$ の格納番地 $h_i(x)$ から $x$ を削除し、代わりに削除の痕跡を表す del を挿入する。

探索

1. はじめに $i=1$ とする。
2. ハッシュテーブルの $h_i(x)$ 番地を参照し、そこに $x$ が格納されていれば $h_i(x)$ が $x$ のアドレスであるので、探索を終了する。
3. $h_i(x)$ に削除を行った履歴である del が入っていた場合、$i=i+1$ として Step2からやり直す。
4. $h_i(x)$ に何も格納されていなかった場合、探索を打ち切る。この場合、$x$ はハッシュ表に格納されていない。

解答（設問４）

線形走査法ではクラスターという現象によって探索の効率が落ちる場合がある。
この現象を説明し、さらに、これを回避する開番地法の別の方法を複数、説明せよ。

開番地法のまとめ を参照

参考

• 福井高専の講義ページ：連鎖法、開番地法
• ブログ：開番地法の詳細
• ブログ：二重ハッシュなど
• 高知工科大学院の講義ページ：二重ハッシュ法など

配点例

設問１,３：各12点
設問２,４：各13点
（50点満点）

{% include foot.html %}

Footnotes

1. $g(x)=1$ とすれば、線形走査法になる ↩