모든 이진 트리는 유일한 전위-중위 순서 쌍을 가진다.
따라서 전위-중위 순서쌍이 주어진다면 트리를 그릴 수 있다!
전략은 서브 트리의 루트를 파악하고, 서브 트리를 계속 그려나가는 것을 계속해서 반복한다!
- 전위 순서를 통해 서브 트리의 루트를 확인한다.
- 중위 순서를 통해 앞서 찾아낸 루트의 왼쪽 서브 트리, 오른쪽 서브 트리를 파악한다.
- 2번에서 찾아낸 서브트리들의 루트를 전위 순서를 통해 확인한다.
- 무한 반복....
(참고)
- 전위 순열: 이진트리를 전위 순회에 따라 방문한 노드들의 순서
- 중위 순열: 이진트리를 중위 순회에 따라 방문한 노드들의 순서
주어진 전위 순서와 중위 순서로 원본 트리를 그려보자!
- 전위 순서: A-B-C-D-E-F-G-H-I
- 중위 순서: B-C-A-E-D-G-H-F-I
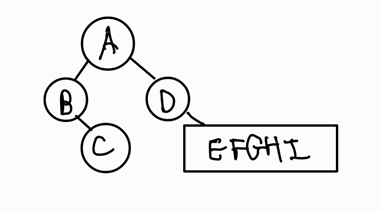
- 전위 순서를 통해 루트가 A임을 파악
- 후위 순서에서 A를 찾는다!
왼편에는 B, C로 구성된 서브 트리! 오른쪽에는 E, D, G, H, F, I로 구성된 서브트리가 있음을 추측할 수 있다.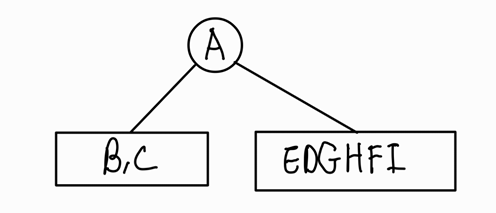
- 이후 B-C의 배치를 추측하는데, 전위 순서에서 B가 먼저 나오므로 B가 왼쪽 서브트리의 루트임
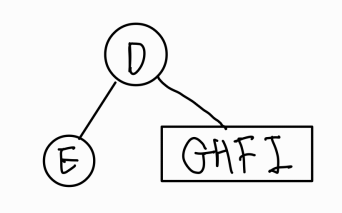
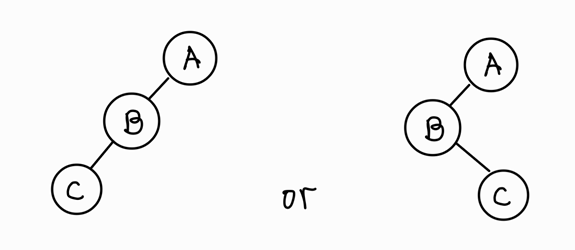4. 중위 순서에서 B-C로 발견되므로, 왼쪽을 틀림! 오른쪽과 같이 구성된다는 것을 알 수 있다!
완성된 모습...
- 전위 순서를 통해 E-D-G-H-F-I의 루트가 D임을 확인!
- 그리고 중위 순서를 통해 D를 루트로 왼쪽은 E 하나만 있고, 오른쪽은 F-G-H-I가 있음을 추측 가능!
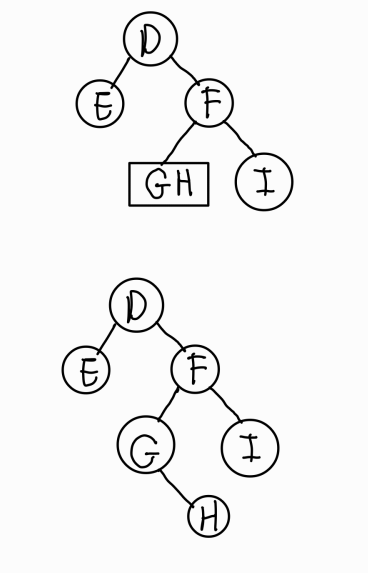
- 전위 순서를 통해 F가 루트임을 확인, 중위 순서를 통해 왼쪽에 G, H 오른 쪽에 I가 옴을 확인
- G-H는 전위 순서를 통해 G가 루트임을 알 수 있었고, 중위 순서를 통해 H는 오른쪽 서브트리에 위치함을 추측 가능하다.
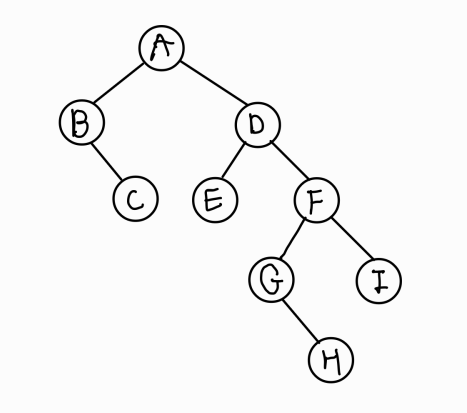
이렇게 전부 합쳐주면 트리가 완성된다!
- n개의 노드를 가진 서로 다른 이진트리의 수
- 1, 2, ..., n의 전위 순열을 가지는 이진트리로 부터 얻을 수 있는 중위 순열의 수
- 1 부터 n까지의 수를 스택에 넣었다가 가능한 모든 방법으로 삭제하여 만들 수 있는 상이한 순열의 수
노하우는, N개의 노드를 가진 이진 트리가 생길 수 있는 모양꼴을 전부 떠올려 본 다음 숫자를 채워 넣는 것이다. 3개의 경우 5개 정도 된다..
- Fundamentals of Data Structures in C++ <HOROWITZ, SAHNI, MEHTA 저>