| comments | difficulty | edit_url | tags | |||
|---|---|---|---|---|---|---|
true |
中等 |
|
给你一座由 n x n 个街区组成的城市,每个街区都包含一座立方体建筑。给你一个下标从 0 开始的 n x n 整数矩阵 grid ,其中 grid[r][c] 表示坐落于 r 行 c 列的建筑物的 高度 。
城市的 天际线 是从远处观察城市时,所有建筑物形成的外部轮廓。从东、南、西、北四个主要方向观测到的 天际线 可能不同。
我们被允许为 任意数量的建筑物 的高度增加 任意增量(不同建筑物的增量可能不同) 。 高度为 0 的建筑物的高度也可以增加。然而,增加的建筑物高度 不能影响 从任何主要方向观察城市得到的 天际线 。
在 不改变 从任何主要方向观测到的城市 天际线 的前提下,返回建筑物可以增加的 最大高度增量总和 。
示例 1:
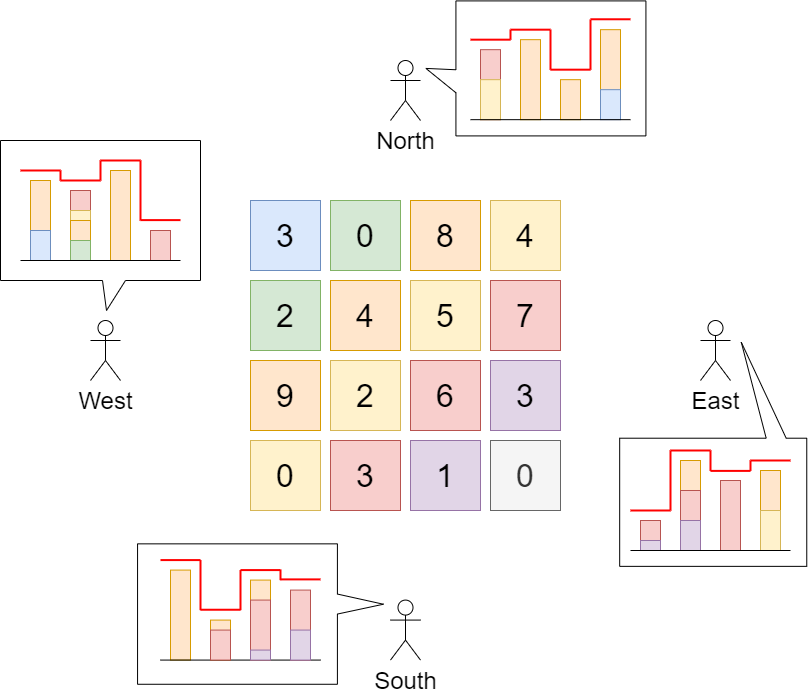
输入:grid = [[3,0,8,4],[2,4,5,7],[9,2,6,3],[0,3,1,0]]
输出:35
解释:建筑物的高度如上图中心所示。
用红色绘制从不同方向观看得到的天际线。
在不影响天际线的情况下,增加建筑物的高度:
gridNew = [ [8, 4, 8, 7],
[7, 4, 7, 7],
[9, 4, 8, 7],
[3, 3, 3, 3] ]
示例 2:
输入:grid = [[0,0,0],[0,0,0],[0,0,0]] 输出:0 解释:增加任何建筑物的高度都会导致天际线的变化。
提示:
n == grid.lengthn == grid[r].length2 <= n <= 500 <= grid[r][c] <= 100
根据题目描述,我们可以将每个单元格
因此,我们可以先遍历一次矩阵,分别计算出每行和每列的最大值,记录在数组
时间复杂度
class Solution:
def maxIncreaseKeepingSkyline(self, grid: List[List[int]]) -> int:
row_max = [max(row) for row in grid]
col_max = [max(col) for col in zip(*grid)]
return sum(
min(row_max[i], col_max[j]) - x
for i, row in enumerate(grid)
for j, x in enumerate(row)
)class Solution {
public int maxIncreaseKeepingSkyline(int[][] grid) {
int m = grid.length, n = grid[0].length;
int[] rowMax = new int[m];
int[] colMax = new int[n];
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
rowMax[i] = Math.max(rowMax[i], grid[i][j]);
colMax[j] = Math.max(colMax[j], grid[i][j]);
}
}
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
ans += Math.min(rowMax[i], colMax[j]) - grid[i][j];
}
}
return ans;
}
}class Solution {
public:
int maxIncreaseKeepingSkyline(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
vector<int> rowMax(m);
vector<int> colMax(n);
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
rowMax[i] = max(rowMax[i], grid[i][j]);
colMax[j] = max(colMax[j], grid[i][j]);
}
}
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
ans += min(rowMax[i], colMax[j]) - grid[i][j];
}
}
return ans;
}
};func maxIncreaseKeepingSkyline(grid [][]int) (ans int) {
rowMax := make([]int, len(grid))
colMax := make([]int, len(grid[0]))
for i, row := range grid {
for j, x := range row {
rowMax[i] = max(rowMax[i], x)
colMax[j] = max(colMax[j], x)
}
}
for i, row := range grid {
for j, x := range row {
ans += min(rowMax[i], colMax[j]) - x
}
}
return
}function maxIncreaseKeepingSkyline(grid: number[][]): number {
const m = grid.length;
const n = grid[0].length;
const rowMax = Array(m).fill(0);
const colMax = Array(n).fill(0);
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
rowMax[i] = Math.max(rowMax[i], grid[i][j]);
colMax[j] = Math.max(colMax[j], grid[i][j]);
}
}
let ans = 0;
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
ans += Math.min(rowMax[i], colMax[j]) - grid[i][j];
}
}
return ans;
}