README_EN.md

comments	difficulty	edit_url	rating	source	tags
true	Medium	https://github.com/doocs/leetcode/edit/main/solution/1300-1399/1319.Number%20of%20Operations%20to%20Make%20Network%20Connected/README_EN.md	1633	Weekly Contest 171 Q3	Depth-First Search Breadth-First Search Union Find Graph

1319. Number of Operations to Make Network Connected

中文文档

Description

There are n computers numbered from 0 to n - 1 connected by ethernet cables connections forming a network where connections[i] = [ai, bi] represents a connection between computers ai and bi. Any computer can reach any other computer directly or indirectly through the network.

You are given an initial computer network connections. You can extract certain cables between two directly connected computers, and place them between any pair of disconnected computers to make them directly connected.

Return the minimum number of times you need to do this in order to make all the computers connected. If it is not possible, return -1.

 

Example 1:

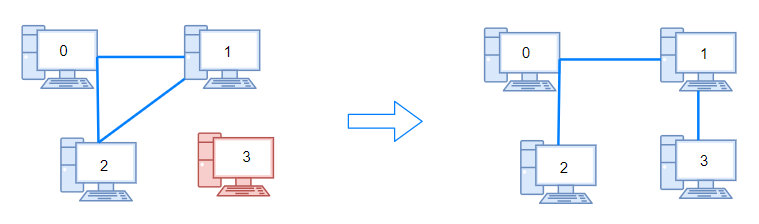
Input: n = 4, connections = [[0,1],[0,2],[1,2]]
Output: 1
Explanation: Remove cable between computer 1 and 2 and place between computers 1 and 3.

Example 2:

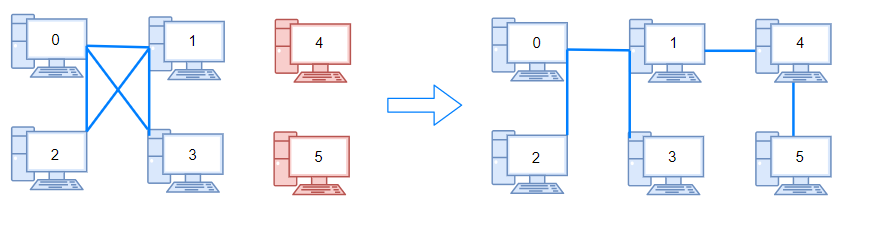
Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
Output: 2

Example 3:

Input: n = 6, connections = [[0,1],[0,2],[0,3],[1,2]]
Output: -1
Explanation: There are not enough cables.

 

Constraints:

• 1 <= n <= 105
• 1 <= connections.length <= min(n * (n - 1) / 2, 105)
• connections[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• There are no repeated connections.
• No two computers are connected by more than one cable.

Solutions

Solution 1: Union-Find

We can use a union-find data structure to maintain the connectivity between computers. Traverse all connections, and for each connection $(a, b)$, if $a$ and $b$ are already connected, then this connection is redundant, and we increment the count of redundant connections. Otherwise, we connect $a$ and $b$, and decrement the number of connected components.

Finally, if the number of connected components minus one is greater than the number of redundant connections, it means we cannot connect all computers, so we return -1. Otherwise, we return the number of connected components minus one.

The time complexity is $O(m \times \log n)$, and the space complexity is $O(n)$. Here, $n$ and $m$ are the number of computers and the number of connections, respectively.

Python3

class Solution:
    def makeConnected(self, n: int, connections: List[List[int]]) -> int:
        def find(x: int) -> int:
            if p[x] != x:
                p[x] = find(p[x])
            return p[x]

        cnt = 0
        p = list(range(n))
        for a, b in connections:
            pa, pb = find(a), find(b)
            if pa == pb:
                cnt += 1
            else:
                p[pa] = pb
                n -= 1
        return -1 if n - 1 > cnt else n - 1

Java

class Solution {
    private int[] p;

    public int makeConnected(int n, int[][] connections) {
        p = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
        }
        int cnt = 0;
        for (int[] e : connections) {
            int pa = find(e[0]), pb = find(e[1]);
            if (pa == pb) {
                ++cnt;
            } else {
                p[pa] = pb;
                --n;
            }
        }
        return n - 1 > cnt ? -1 : n - 1;
    }

    private int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}

C++

class Solution {
public:
    int makeConnected(int n, vector<vector<int>>& connections) {
        vector<int> p(n);
        iota(p.begin(), p.end(), 0);
        int cnt = 0;
        function<int(int)> find = [&](int x) -> int {
            if (p[x] != x) {
                p[x] = find(p[x]);
            }
            return p[x];
        };
        for (const auto& c : connections) {
            int pa = find(c[0]), pb = find(c[1]);
            if (pa == pb) {
                ++cnt;
            } else {
                p[pa] = pb;
                --n;
            }
        }
        return cnt >= n - 1 ? n - 1 : -1;
    }
};

Go

func makeConnected(n int, connections [][]int) int {
	p := make([]int, n)
	for i := range p {
		p[i] = i
	}
	cnt := 0
	var find func(x int) int
	find = func(x int) int {
		if p[x] != x {
			p[x] = find(p[x])
		}
		return p[x]
	}
	for _, e := range connections {
		pa, pb := find(e[0]), find(e[1])
		if pa == pb {
			cnt++
		} else {
			p[pa] = pb
			n--
		}
	}
	if n-1 > cnt {
		return -1
	}
	return n - 1
}

TypeScript

function makeConnected(n: number, connections: number[][]): number {
    const p: number[] = Array.from({ length: n }, (_, i) => i);
    const find = (x: number): number => {
        if (p[x] !== x) {
            p[x] = find(p[x]);
        }
        return p[x];
    };
    let cnt = 0;
    for (const [a, b] of connections) {
        const [pa, pb] = [find(a), find(b)];
        if (pa === pb) {
            ++cnt;
        } else {
            p[pa] = pb;
            --n;
        }
    }
    return cnt >= n - 1 ? n - 1 : -1;
}