Skip to content

Latest commit

 

History

History
233 lines (177 loc) · 7.92 KB

README.md

File metadata and controls

233 lines (177 loc) · 7.92 KB
comments difficulty edit_url rating source tags
true
困难
2267
第 125 场双周赛 Q4
贪心
位运算
树
数组
动态规划
排序

3068. 最大节点价值之和

English Version

题目描述

给你一棵 n 个节点的 无向 树，节点从 0 到 n - 1 编号。树以长度为 n - 1 下标从 0 开始的二维整数数组 edges 的形式给你，其中 edges[i] = [ui, vi] 表示树中节点 ui 和 vi 之间有一条边。同时给你一个 正 整数 k 和一个长度为 n 下标从 0 开始的 非负 整数数组 nums ，其中 nums[i] 表示节点 i 的 价值 。

Alice 想 最大化 树中所有节点价值之和。为了实现这一目标，Alice 可以执行以下操作 任意 次（包括 0 次）：

  • 选择连接节点 u 和 v 的边 [u, v] ，并将它们的值更新为： 
    <ul>
	<li><code>nums[u] = nums[u] XOR k</code></li>
	<li><code>nums[v] = nums[v] XOR k</code></li>
</ul>
</li>

请你返回 Alice 通过执行以上操作 任意次 后，可以得到所有节点 价值之和 的 最大值 。

 

示例 1：

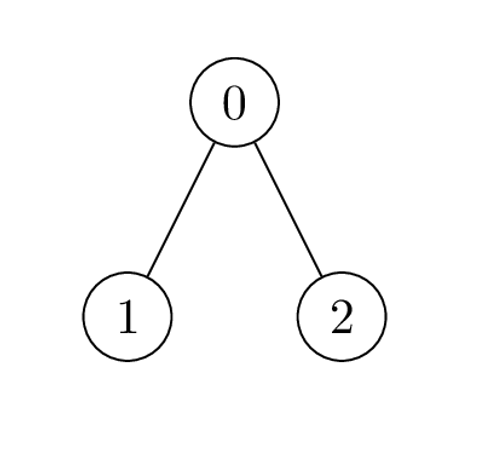
输入：nums = [1,2,1], k = 3, edges = [[0,1],[0,2]]
输出：6
解释：Alice 可以通过一次操作得到最大价值和 6 ：
- 选择边 [0,2] 。nums[0] 和 nums[2] 都变为：1 XOR 3 = 2 ，数组 nums 变为：[1,2,1] -> [2,2,2] 。
所有节点价值之和为 2 + 2 + 2 = 6 。
6 是可以得到最大的价值之和。

示例 2：

输入：nums = [2,3], k = 7, edges = [[0,1]]
输出：9
解释：Alice 可以通过一次操作得到最大和 9 ：
- 选择边 [0,1] 。nums[0] 变为：2 XOR 7 = 5 ，nums[1] 变为：3 XOR 7 = 4 ，数组 nums 变为：[2,3] -> [5,4] 。
所有节点价值之和为 5 + 4 = 9 。
9 是可以得到最大的价值之和。

示例 3：

输入：nums = [7,7,7,7,7,7], k = 3, edges = [[0,1],[0,2],[0,3],[0,4],[0,5]]
输出：42
解释：Alice 不需要执行任何操作，就可以得到最大价值之和 42 。

 

提示：

  • 2 <= n == nums.length <= 2 * 104
  • 1 <= k <= 109
  • 0 <= nums[i] <= 109
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= edges[i][0], edges[i][1] <= n - 1
  • 输入保证 edges 构成一棵合法的树。

解法

方法一：动态规划

对于任意一个数 $x$，与 $k$ 异或偶数次后，值不变。所以，对于一棵树的任意一条路径，我们将路径上所有的边都进行操作，那么该路径上除了起点和终点外，其他节点的值都不会改变。

另外，无论进行了多少次操作，总会有偶数个元素异或了 $k$，其余元素不变。

因此，问题转化为：对于数组 $\textit{nums}$，任选其中偶数个元素异或 $k$，使得和最大。

我们可以使用动态规划解决这个问题。设 $f_0$ 表示当前有偶数个元素异或了 $k$ 时的最大和，而 $f_1$ 表示当前有奇数个元素异或了 $k$ 时的最大和。那么状态转移方程为：

$$ \begin{aligned} f_0 &= \max(f_0 + x, f_1 + (x \oplus k)) \\ f_1 &= \max(f_1 + x, f_0 + (x \oplus k)) \end{aligned} $$

其中 $x$ 表示当前元素的值。

我们遍历数组 $\textit{nums}$，根据上述状态转移方程更新 $f_0$ 和 $f_1$，最后返回 $f_0$ 即可。

时间复杂度 $O(n)$，其中 $n$ 为数组 $\textit{nums}$ 的长度。空间复杂度 $O(1)$。

Python3

class Solution:
    def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:
        f0, f1 = 0, -inf
        for x in nums:
            f0, f1 = max(f0 + x, f1 + (x ^ k)), max(f1 + x, f0 + (x ^ k))
        return f0

Java

class Solution {
    public long maximumValueSum(int[] nums, int k, int[][] edges) {
        long f0 = 0, f1 = -0x3f3f3f3f;
        for (int x : nums) {
            long tmp = f0;
            f0 = Math.max(f0 + x, f1 + (x ^ k));
            f1 = Math.max(f1 + x, tmp + (x ^ k));
        }
        return f0;
    }
}

C++

class Solution {
public:
    long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {
        long long f0 = 0, f1 = -0x3f3f3f3f;
        for (int x : nums) {
            long long tmp = f0;
            f0 = max(f0 + x, f1 + (x ^ k));
            f1 = max(f1 + x, tmp + (x ^ k));
        }
        return f0;
    }
};

Go

func maximumValueSum(nums []int, k int, edges [][]int) int64 {
	f0, f1 := 0, -0x3f3f3f3f
	for _, x := range nums {
		f0, f1 = max(f0+x, f1+(x^k)), max(f1+x, f0+(x^k))
	}
	return int64(f0)
}

TypeScript

function maximumValueSum(nums: number[], k: number, edges: number[][]): number {
    let [f0, f1] = [0, -Infinity];
    for (const x of nums) {
        [f0, f1] = [Math.max(f0 + x, f1 + (x ^ k)), Math.max(f1 + x, f0 + (x ^ k))];
    }
    return f0;
}

Rust

impl Solution {
    pub fn maximum_value_sum(nums: Vec<i32>, k: i32, edges: Vec<Vec<i32>>) -> i64 {
        let mut f0: i64 = 0;
        let mut f1: i64 = i64::MIN;

        for &x in &nums {
            let tmp = f0;
            f0 = std::cmp::max(f0 + x as i64, f1 + (x ^ k) as i64);
            f1 = std::cmp::max(f1 + x as i64, tmp + (x ^ k) as i64);
        }

        f0
    }
}

C#

public class Solution {
    public long MaximumValueSum(int[] nums, int k, int[][] edges) {
        long f0 = 0, f1 = -0x3f3f3f3f;
        foreach (int x in nums) {
            long tmp = f0;
            f0 = Math.Max(f0 + x, f1 + (x ^ k));
            f1 = Math.Max(f1 + x, tmp + (x ^ k));
        }
        return f0;
    }
}