斯坦福CS231n笔记
+ TomatoEater 2022年7月 +
看的是b站的视频,是2017年的版本。CS231n的全称是CS231n: Convolutional Neural Networks for Visual Recognition,即面向视觉识别的卷积神经网络。笔记前面很多内容参考了知乎。
然而从第五章开始我就看密西根大学的EECS 498-007/598-005的2019版本的课了,个人觉得讲的更加清晰一点。
个人觉得作为初学者来说,本课程还是有一定难度的,无论是来自于话题的不熟悉、Justin Johnson的语速,还是numpy、pytorch的陌生。但是课程质量还是很高的,其中三个assignment相当不错的(虽然大部分我都不是自己写的)。
作为初学者,笔记纰漏难免。
一、简介
对于一张图片,人看到的是图片,计算机看到的是一个三维向量,每个数据范围在0~255。这就是所谓人与计算机之间的semantic gap。注意到我们用RGB格式,且每个颜色有8位,所以数据范围在0~255之间;像素构成两维,RGB构成第三维。下面是一个两行五列的色块:
1[[[188 71 38]2 [254 113 0]3 [226 127 0]4 [132 91 39]5 [ 28 46 84]]6 7 [[118 12 112]8 [202 65 59]9 [242 110 27]10 [218 111 29]11 [151 89 38]]]注意到这些多维数组,我们称之为张量(tensor)。
计算机识别图像遇到困难和挑战有:
- 视角变化(Viewpoint variation):同一个物体,摄像机可以从多个角度来展现。
- 大小变化(Scale variation):物体可视的大小通常是会变化的(不仅是在图片中,在真实世界中大小也是变化的)。
- 形变(Deformation):很多东西的形状并非一成不变,会有很大变化。
- 遮挡(Occlusion):目标物体可能被挡住。有时候只有物体的一小部分(可以小到几个像素)是可见的。
- 光照条件(Illumination conditions):在像素层面上,光照的影响非常大。
- 背景干扰(Background clutter):物体可能混入背景之中,使之难以被辨认。
- 类内差异(Intra-class variation):一类物体的个体之间的外形差异很大,比如椅子。这一类物体有许多不同的对象,每个都有自己的外形。
我们必须实现一个具有较好鲁棒性的算法来应对以上问题。
那如何写一个图像分类的算法呢?我们采用数据驱动方法——给计算机很多数据,然后实现学习算法。也就是先手动给数据分好类、打好标签,做出训练集;然后实现训练函数,来训练分类器(train the classifier)或者说学习一个模型;最后实现预测函数,利用训练好的分类器来预测它未曾见过的图像的分类标签。所谓的分类器就是:在标记好类别的训练数据基础上,判断一个新的观察样本所属的类别。
二、Nearest Neighbor以及k-NN分类器
1. Nearest Neighbor分类器
思路:训练时记下所有图像,且不做更多处理;预测则通过遍历所有图像后,找出距离最近的那幅图像,并返回该图像的标签。
时间复杂度:训练O(1);预测O(n)(这里意指要遍历n张图像)
应用情况:几乎不使用,预测时间过长,预测精度差
距离:距离有两种——L1距离(曼哈顿距离)、L2距离(欧式距离)。前者是矩阵中所有数据做差后加和,后者是矩阵所有数据做差后做平方和后开根。L1距离随坐标的选取而不同,L2距离和坐标无关。因此,若坐标有特定含义,可以优先考虑L1距离。
数据集:CIFAR-10。这个数据集包含了60000张32X32的图像。每张图像都有10种分类标签中的一种。其中50000张为训练集,10000张为测试集。
python代码:
1)加载数据。在下面的代码中,Xtr(大小是50000x32x32x3,50000个三维向量)存有训练集中所有的图像;Ytr是对应的长度为50000的1维数组,存有图像对应的分类标签(从0到9);tr意为train训练数据,te意为test测试数据;Xtr.shape[0] = 50000, Xte.shape[0] = 10000;Xtr、Ytr、Xte、Yte应该都是numpy中的array数据类型。
xxxxxxxxxx41Xtr, Ytr, Xte, Yte = load_CIFAR10('data/cifar10/') # a magic function we provide2# flatten out all images to be one-dimensional3Xtr_rows = Xtr.reshape(Xtr.shape[0], 32 * 32 * 3) # Xtr_rows becomes 50000个模为3072的一维向量4Xte_rows = Xte.reshape(Xte.shape[0], 32 * 32 * 3) # Xte_rows becomes 10000个模为3072的一维向量2)训练和评分。在下面代码中,Yte_predict == Yte返回的是一个布尔数组,np.mean返回数组里所有元素的平均值。
xxxxxxxxxx61nn = NearestNeighbor() # create a Nearest Neighbor classifier class2nn.train(Xtr_rows, Ytr) # train the classifier on the training images and labels3Yte_predict = nn.predict(Xte_rows) # predict labels on the test images4# and now print the classification accuracy, which is the average number5# of examples that are correctly predicted (i.e. label matches)6print('accuracy: %f' % (np.mean(Yte_predict == Yte)))3)上述代码中NearestNeighbor类为:
x1import numpy as np2
+3class NearestNeighbor(object):4 def __init__(self):5 pass6
+7 def train(self, X, y):8 """ X is N x D where each row is an example. Y is 1-dimension of size N """9 # the nearest neighbor classifier simply remembers all the training data10 self.Xtr = X11 self.ytr = y12
+13 def predict(self, X):14 """ X is N x D where each row is an example we wish to predict label for """15 num_test = X.shape[0]16 # lets make sure that the output type matches the input type17 Ypred = np.zeros(num_test, dtype = self.ytr.dtype)18
+19 # loop over all test rows20 for i in range(num_test):21 # find the nearest training image to the i'th test image22 # using the L1 distance (sum of absolute value differences)23 distances = np.sum(np.abs(self.Xtr - X[i,:]), axis = 1)24 # or using the L2 distance, 事实上就比较大小而言不必开方25 # distances = np.sqrt(np.sum(np.square(self.Xtr - X[i,:]), axis = 1))26 min_index = np.argmin(distances) # get the index with smallest distance27 Ypred[i] = self.ytr[min_index] # predict the label of the nearest example28
+29 return Ypred30
+2. k-NN分类器
k-NN是k-Nearest Neighbor的缩写,当k等于一时,就是Nearest Neighbor分类器。
思路:找距离最近的k张图片,选取这k张照片出现次数最多的标签作为预测结果。
相对优势:如下图所示,更高的k值可以让分类的效果更平滑,使得分类器对于异常值更有抵抗力。白色区域应该是近邻标签的最高票数相同导致的(比如:2个邻居是红色,2个邻居是蓝色,还有1个是绿色),此时可以任意选择其中一个标签作为预测结果。
应用情况:几乎不使用,预测时间过长,预测精度差

如何选择k:
- 超参数:在机器学习的上下文中,超参数(hyperparameter)是在开始学习过程之前设置值的参数,而不是通过训练得到的参数数据。通常情况下,需要对超参数进行优化,选择一组最优超参数,以提高学习的性能和效果。而k、L1L2距离就是超参数。
- 常见做法:将所有数据分为——训练集、验证集和测试集。通过验证集来选取最佳的k值,然后用这个k来跑一次测试集。以CIFAR-10为例,我们可以用49000个图像作为训练集,用1000个图像作为验证集。
- 另一种做法:交叉验证(cross validation):先把所有数据分为训练集和测试集;再把训练集平分(3份或5份或10份之类的),依次取其中一份作为验证集,其余作为训练集;然后取所有验证结果的平均值作为结果;最后找到最优的k值跑一次测试集。优劣:当数据量较小时可以采用;耗费较多的计算资源。
3. 总评
眼想想就很一般——存储训练数据占用空间大、预测函数计算资源耗时高、预测准确度低。
具体说来,这些图片的排布更像是一种颜色分布函数,或者说是基于背景的,而不是图片的语义主体。比如,狗的图片可能和青蛙的图片非常接近,这是因为两张图片都是白色背景。从理想效果上来说,我们肯定是希望同类的图片能够聚集在一起,而不被背景或其他不相关因素干扰。为了达到这个目的,我们不能止步于原始像素比较,得继续前进。
三、线性分类器
1. 简介
考虑这样一个函数,输入一张图像,输出其对应每个标签的评分,选取最高的评分,便是预测结果。这就是评分函数(score function)。那么如何评价评分结果的好坏、如何量化预测分类标签和真实标签的一致性,我们需要损失函数(loss function)。于是,我们再通过一些手段不断改进评分函数中的参数,让损失函数值最小,这便是最优化问题。我们本节的思路就将围绕这三点展开。
此外,损失函数也被称为代价函数(cost function)或目标函数(objective)。
2. 线性评分函数
考虑这样一个线性映射:
举例:仍以CIFAR-10为例。

此外还有两个技巧:
偏差和权重合并(bias trick)。只用在列向量
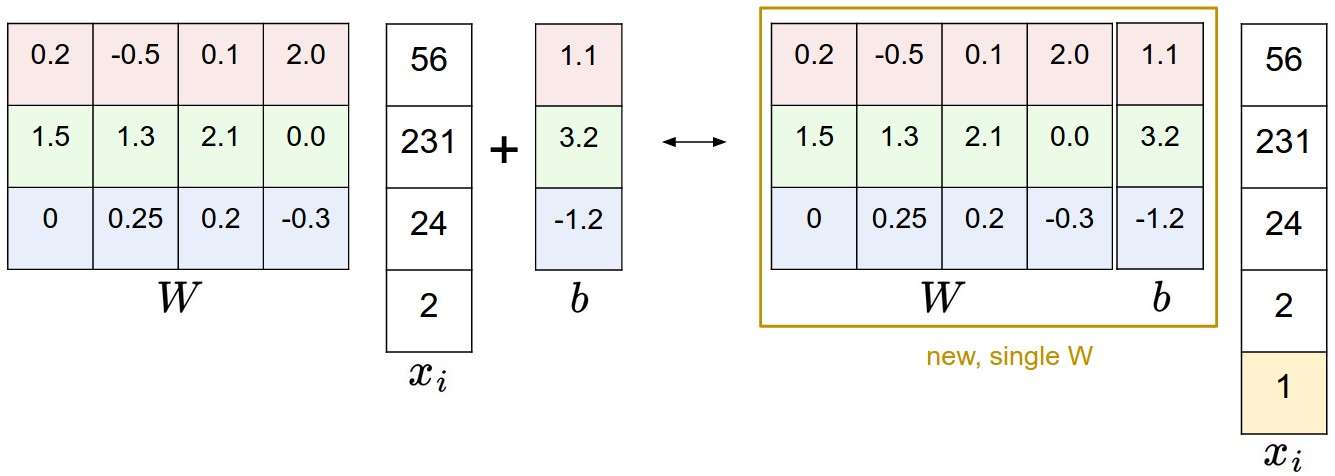
图像数据预处理
- 中心化:数值减去均值,使得新的数据平均数为0
- 标准化/归一化:数值减去均值,再除以标准差,使得新的数据平均数为0,且方差为1
3. 损失函数
这里先介绍两种损失函数,第一个是SVM(support vector machine, 支持向量机)分类器采用的合页损失(hinge loss),第二个是Softmax分类器采用的交叉熵损失(cross-entropy loss)。然后介绍正则化(regularization)。事实上,目前我并没有理清楚这些奇怪的命名,以及前应后果的联系。可能要学完机器学习才能理清思路吧。不过缺少背景知识不妨碍我去学习这两种损失函数,这里希望建立一种感性认识。
此外,我对这部分的内容进行了顺序调整,尽可能理清楚思路吧。
目前是这么理解SVM的:SVM利用决策边界划分两类数据。数据是n维的话,那么决策边界是n-1维。若决策边界大于三维的话,这个决策边界可以称为超平面,划分也称为超平面划分。我们只考虑线性SVM,对于那些不是线性可分的数据,可以通过核技巧(kernel trick)来转换为线性可分的情况。而找到这样的核函数很难,有时就放宽对样本的要求,允许少量的样本分类错误,这就是所谓的软间隔。在软间隔中,有一个损失函数也就是合页损失函数,来评价样本背离约束的情况。现在我们要分割超过两类的数据,SVM要推广到多类SVM(multiclass SVM)。SVM深入学习需要凸优化的背景知识。
3.1 损失函数
损失函数的最终表达式如下:
上述公式由两个部分组成:数据损失(data loss),即所有样例的的平均损失,以及正则化损失(regularization loss)。下面先介绍两种
3.2 SVM分类器
将第
其中
又
例子:假设有3个分类,评分
即此时数据损失为8
解释:只有当不正确标签的分数比正确类别分数高出
此外,还有平方合页损失函数(也就是
一些课堂提问:
- 若初始化W各元素很小,所以每个分数都差不多在0左右,那么
- 如果在计算时没有限制
- 如果求平均而不是简单加和,损失函数性质不变(仍然是线性的);但是如果是平方合页损失函数了,就是不同的损失函数了
- 如何设置
python代码:
xxxxxxxxxx371# 版本一:非向量化2def L_i(x, y, W):3 """4 unvectorized version. Compute the multiclass svm loss for a single example (x,y)5 - x is a column vector representing an image (e.g. 3073 x 1 in CIFAR-10)6 with an appended bias dimension in the 3073-rd position (i.e. bias trick)7 - y is an integer giving index of correct class (e.g. between 0 and 9 in CIFAR-10)8 - W is the weight matrix (e.g. 10 x 3073 in CIFAR-10)9 """10 delta = 1.0 # see notes about delta later in this section11 # A.dot(B)就是矩阵A、B乘积AB12 scores = W.dot(x) # scores becomes of size 10 x 1, the scores for each class13 correct_class_score = scores[y]14 D = W.shape[0] # number of classes, e.g. 1015 loss_i = 0.016 for j in range(D):17 if j == y:18 continue19 loss_i += max(0, scores[j] - correct_class_score + delta)20 return loss_i21
+22# 版本二:半向量化,利用广播机制,更快、更简单23def L_i_vectorized(x, y, W):24 """25 A faster half-vectorized implementation. half-vectorized26 refers to the fact that for a single example the implementation contains27 no for loops, but there is still one loop over the examples (outside this function)28 """29 delta = 1.030 scores = W.dot(x)31 # compute the margins for all classes in one vector operation32 margins = np.maximum(0, scores - scores[y] + delta)33 # on y-th position scores[y] - scores[y] canceled and gave delta. We want34 # to ignore the y-th position and only consider margin on max wrong class35 margins[y] = 036 loss_i = np.sum(margins)37 return loss_i3.3 Softmax 分类器
Softmax分类器其实是logistic回归分类器面对多个分类的一般化归纳(我显然看不懂这句话)。损失函数就是所谓的交叉熵损失(cross-entropy loss)(交叉熵的背景知识这里也不再研究)。公式如下:
上式中将第
例子:
一些课堂提问:
- Softmax函数范围是0~1
- 若初始化W各元素很小,所以每个分数都差不多在0左右,那么
3.4 Softmax vs. SVM
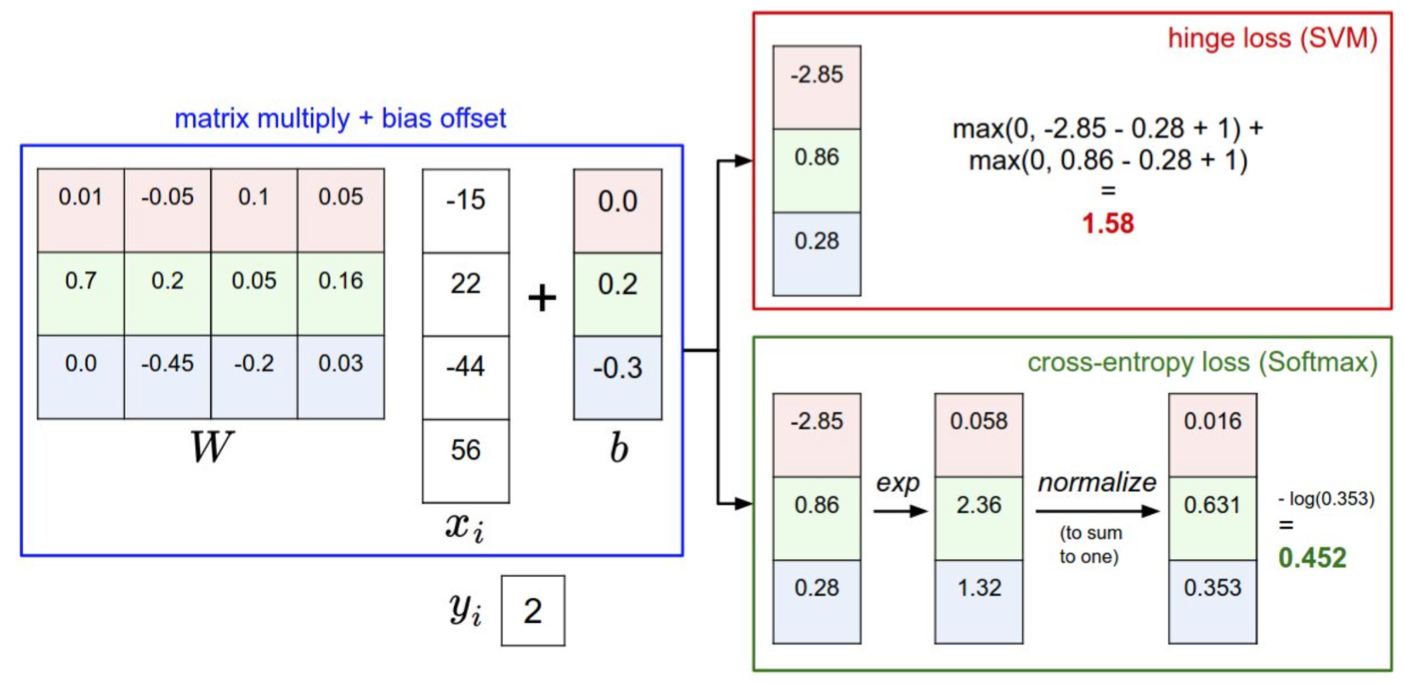
- 分值的解释不同:SVM分类器将它们看做是分类评分,它的损失函数鼓励正确的分类的分值比其他分类的分值高出至少一个边界值。Softmax分类器将这些数值看做是每个分类没有归一化的对数概率,鼓励正确分类的归一化的对数概率变高,其余的变低。
- SVM对于数字个体的细节是不关心的,Softmax分类器对于分数是永远不会满意的
3.5 正则化损失
若存在一个权重W能够正确地分类每个数据,即对于所有的
为了避免训练时过拟合,我们向损失函数增加一个正则化惩罚(regularization penalty)
常用正则化
- L2 正则化:
- L1 正则化:
式中
例子:假设输入向量的L2惩罚是
更好,因为它的正则化损失更小。
L1和L2的感性区别:L1更倾向于稀疏解,它倾向于让W大部分元素接近0;而L2更多考虑W整体分布,倾向于更小更分散的权重向量,这就会鼓励分类器最终将所有维度上的特征都用起来,而不是强烈依赖其中少数几个维度。
3.6 实际考虑
如何设置
你可能注意到上面的内容对超参数
4. 最优化
最优化的目的是寻找参数W,它使得损失函数值最小。
优化的方法很多,但是我们直接进入梯度下降。
4.1 梯度计算
有两种梯度:一是数值梯度(numerical gradient),缓慢的近似方法,但实现相对简单。另一个是解析梯度(analytic gradient),计算迅速、结果精确,但是实现时容易出错,且需要使用微分。现在对两种方法进行介绍:
数值梯度。采用有限差分法(finite difference method)计算,主要思想就是利用梯度定义近似计算。比如当前权重W是[[0.34, -1.11], [2.14, -8.28]]、当前损失值是1.25347,现在将W改称[[0.3401, -1.11], [2.14, -8.28]],得到新的损失值是1.25322。由此可以算出梯度的第一个元素为
解析梯度。先算出梯度的表达式,再带入数值。以SVM为例,仍约定权重W第j行记作
对
又损失函数的梯度为:
带入数据即可。结果是一个和W大小相同的矩阵。
建议:利用解析梯度计算,利用数据梯度检查。说人话:先手动求出梯度解析式,然后带入特殊值检验一下。
数值梯度的python实现:
xxxxxxxxxx301def eval_numerical_gradient(f, x):2 """ 3 一个f在x处的数值梯度法的简单实现4 - f是只有一个参数的函数5 - x是计算梯度的点,10X30736 """ 7
+8 fx = f(x) # 计算函数值9 grad = np.zeros(x.shape) # grad初始化为x的大小,但是元素都为010 h = 0.0000111
+12 # 对x中所有的索引进行迭代13 it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])14 while not it.finished:15
+16 # 计算x+h处的函数值17 ix = it.multi_index18 old_value = x[ix]19 x[ix] = old_value + h # 增加h20 fxh = f(x) # 计算f(x + h)21 x[ix] = old_value # 恢复到前一个值22
+23 # 计算偏导数24 grad[ix] = (fxh - fx) / h # 坡度25 it.iternext() # 到下个维度26
+27 return grad28
+29# 传入损失函数和权重,即得损失函数关于权重的梯度30df = eval_numerical_gradient(loss_fun, W)解析梯度的函数原型
xxxxxxxxxx21def evaluate_gradient(loss_fun, data, weights)2# 要传入损失函数,照片data数据,权重4.2 梯度下降
计算出梯度,就需要选取步长(step size,也叫做学习率learning rate),还要注意到梯度是指向函数增加的方向,所以最后是减去梯度乘以步长。步长也是一个超参数,而且相当重要,可能是最先需要确定的超参数。小步长下降稳定但进度慢,大步长进展快但是风险更大。采取大步长可能导致错过最优点,让损失值上升。
梯度下降有以下几种版本:
(full) batch gradient descent
xxxxxxxxxx31while True:2weights_grad = evaluate_gradient(loss_fun, data, weights)3weights += - step_size * weights_gradevaluate_gradient应该是对每个data数据分别算出权重weights的梯度,然后求和。
小批量数据梯度下降(Mini-batch gradient descent):当训练数据很多时,为了加快训练,只选择训练集中的小批量(mini-batch)数据。一个典型的小批量包含32/64/128/256个例子,而整个训练集有一百二十万个。小批量数据的大小是一个超参数,但是一般并不需要通过交叉验证来调参。它一般由存储器的限制来决定的。之所以使用2的指数,是因为在实际中许多向量化操作实现的时候,如果输入数据量是2的倍数,那么运算更快。
xxxxxxxxxx51# 普通的小批量数据梯度下降2while True:3data_batch = sample_training_data(data, 256) # 256个数据4weights_grad = evaluate_gradient(loss_fun, data_batch, weights)5weights += - step_size * weights_grad # 参数更新随机梯度下降(Stochastic Gradient Descent 简称SGD):指每个批量中只有1个数据样本的小批量数据梯度下降,有时候也被称为在线梯度下降。这种策略在实际情况中相对少见,因为向量化操作的代码一次计算100个数据 比100次计算1个数据要高效很多。即使SGD在技术上是指每次使用1个数据来计算梯度,你还是会听到人们使用SGD来指代小批量数据梯度下降(事实上本课程(包括本整理)中SGD就是指小批量数据梯度下降)。
4.3 SGD的问题
当损失值在一个维度上改变很快,而另一个维度改变很慢,则会一个维度更新缓慢且另一个维度反复抖动。考虑下面一个两元函数(类似等高线图)的更新:

有极小值点和鞍点,梯度不再更新
有噪声,梯度乱跑,如下图

4.4 SGD + Momentum
常见且推荐的方法。就是之前的速度会影响之后的。下图中

显然的,引入动量可以一定程度上解决4.3节SGD具有的三个问题。
4.5 Nesterov Momentum
另一种动量形式,计算
为了更好贴合梯度计算api,有以下等价形式:

三种方法对比如下:(可以看到引入动量后权重的更新会overshoot——跑过头再回来)

4.6 AdaGrad
AdaGrad(adaptive gradient)出发点在于想让历史上大梯度的权重更新慢一点、历史上小梯度的权重更新快一点。代码如下:
xxxxxxxxxx81# AdaGrad2grad_squared = 0 # 记录权重中每个元素的梯度平方和3for t in range(nun_steps):4 dw = compute_gradient(w) # 梯度矩阵5 grad_squared += dw * dw # 梯度矩阵中每个元素各自平方,加到grad_squared中6 # 更新梯度时,梯度矩阵每个元素除以各自的历史上平方和开根7 # 显然历史上大梯度的将除以较大的值,降低其更新速度8 w -= learning_rate * dw / (grad_squared.sqrt() + 1e-7)4.7 RMSProp
当AdaGrad运行时间较长后,grad_squared会变得很大,导致梯度不再更新了。针对这个问题,只需让grad_squared更新为之前值和新加入的dw*dw的加权,称之为RMSProp(root mean square propagation)。代码如下:
xxxxxxxxxx61# RMSProp2grad_squared = 03for t in range(nun_steps):4 dw = compute_gradient(w)5 grad_squared = decay_rate * grad_squared + (1 - decay_rate) * dw * dw # key6 w -= learning_rate * dw / (grad_squared.sqrt() + 1e-7)RMSProp相较于动量,更新权重时不容易overshoot。
4.8 Adam
很常见且推荐使用的一个方法,综合利用了RMSProp和Momentum两个想法,代码如下:
xxxxxxxxxx91moment1 = 02moment2 = 03for t in range(num_steps):4 dw = compute_gradient(w)5 moment1 = beta1 * moment1 + (1 - beta1) * dw # momentum6 moment2 = beta2 * moment2 + (1 - beta2) * dw * dw # RMSProp7 moment1_unbias = moment1 / (1 - beta1 ** t) # bias correction8 moment2_unbias = moment2 / (1 - beta2 ** t) # bias correction9 w -= learning_rate * moment1_unbias / (moment2_unbias.sqrt() + 1e-7)通常设置beta1=0.9、beta2=0.999、learning_rate=1e-3,5e-4,1e-4。之所以要bias correction是出于以下考虑:在开始训练时,moment2可能是一个很小的值,导致权重的更新过大。几种方法模拟如下:

4.9 Second-Order Optimization
之前我们讨论的梯度下降法都只用了一阶导,称为first-order optimization。还有利用一阶和二阶导来更新的,似乎用了向量函数的泰勒展开,引入Hessian矩阵。但是由于它在时间和空间上的糟糕表现,并不是一个可行的方案。这里也不再展开了。
四、反向传播
反向传播(backpropagation)是一种求梯度的方法。其背后的数学背景就是链式法则(chain rule)。下面通过几个例子来进行说明。
需要申明一个不严格但是常用的术语,常常用“x上的梯度”或者“x的梯度”来表示“函数对于x的偏导”。
1. 例一
本例希望建立反向传播的基本概念。
例一:求
步骤一:将函数f可视化为计算图(computational graph),(先忽略掉绿色和红色的数字)
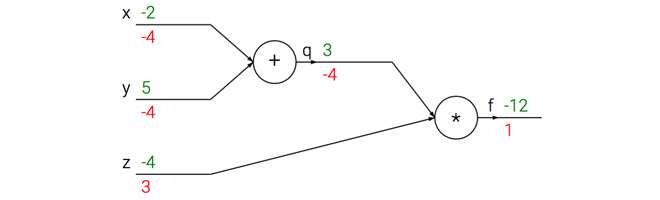
步骤二:前向传播计算出每个节点的数值,如上图绿色数字所示
步骤三:反向传播计算每个节点上的梯度,如上图红色数字所示。下面对步骤三进一步阐释。
- 最右侧
- 由
- 由
步骤四:计算图中最左侧(-4,-4,3)即为所求。
注意到:
- 计算函数对一个节点的偏导时,只需用局部梯度(local gradient)乘以上游梯度(upstream gradient)。比如计算上图对x的偏导,上游梯度是-4,局部梯度是1.
- 若把运算符节点称为门,那么反向传播可以看做是门单元之间在通过梯度信号相互通信。比如加法门单元相当于分配器distributor,把输出的梯度相等地分发给它所有的输入,来作为他们的梯度;取最大值门单元相当于路由router,将梯度转给其中大的那个输入,而小的那个输入的梯度为零;乘法门单元相当于交换器switcher,将输入乘以上游梯度后,再交换分发给输入,来作为他们的梯度。
python代码:
xxxxxxxxxx141# 设置输入值2x = -2; y = 5; z = -43
+4# 进行前向传播5q = x + y # q becomes 36f = q * z # f becomes -127
+8# 进行反向传播:9# 首先回传到 f = q * z10dz = q # df/dz = q, 所以关于z的梯度是311dq = z # df/dq = z, 所以关于q的梯度是-412# 现在回传到q = x + y13dx = 1.0 * dfdq # dq/dx = 1. 这里的乘法是因为链式法则14dy = 1.0 * dfdq # dq/dy = 12. 例二
本例希望建立起多个门组合成一个门的想法。
对于有计算图:
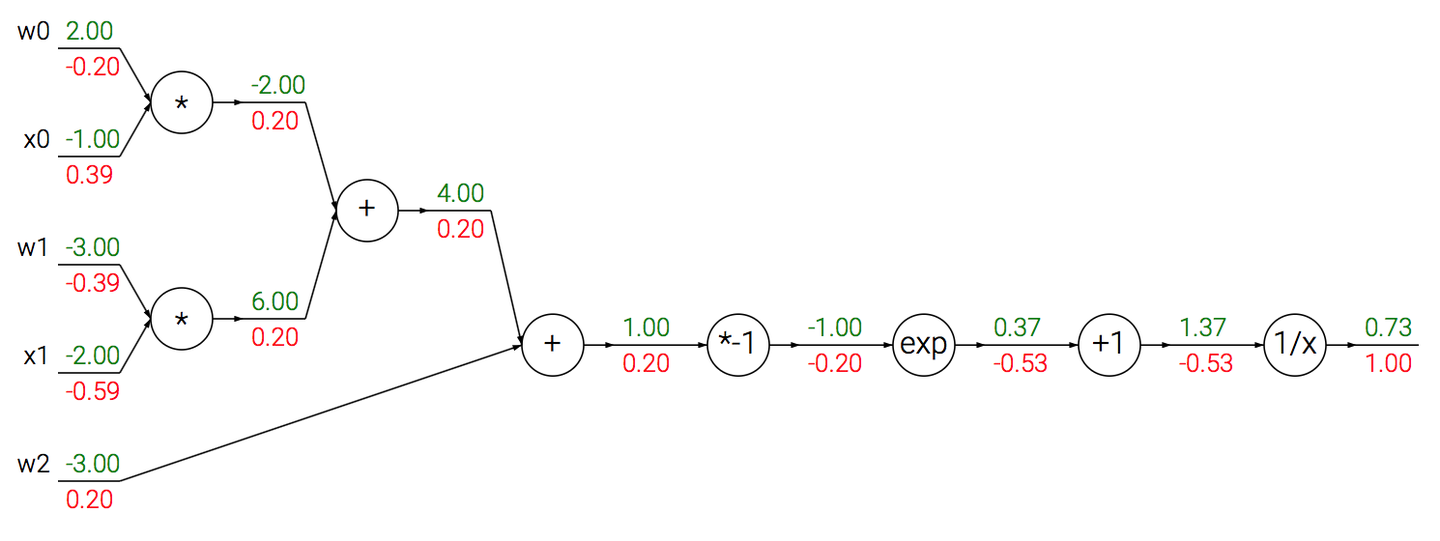
略作说明,比如exp节点。已知输入值x=-1,输出q=ex=0.37,q上的梯度是-0.53,求x上的梯度。解:
而。sigmoid对x求导有:
于是计算图中最后四个门可以简化为一个门,且局部梯度为(1-0.73)*0.73=0.20。这样的处理可以简化运算。
python代码:
xxxxxxxxxx111w = [2,-3,-3] # 假设一些随机数据和权重2x = [-1, -2]3
+4# 前向传播5dot = w[0]*x[0] + w[1]*x[1] + w[2]6f = 1.0 / (1 + math.exp(-dot)) # sigmoid函数7
+8# 对神经元反向传播9ddot = (1 - f) * f # 点积变量的梯度, 使用sigmoid函数求导10dx = [w[0] * ddot, w[1] * ddot] # 回传到x11dw = [x[0] * ddot, x[1] * ddot, 1.0 * ddot] # 回传到w注意到上面已经有矩阵和向量的影子了。例三将进一步阐明这种情况。
3. 例三
之前考虑的内容都是多元函数的情况,本例希望将其推广到矩阵和向量操作。这里只给出最难的矩阵相乘的例子。
例三:假设我们已经知道输入矩阵W(大小为5*10)、输入矩阵X(大小为10*3)、输出矩阵D=WX(大小为5*3)、以及D的梯度dD(大小为5*3),现在想要计算W和X的梯度。
先上python代码:
xxxxxxxxxx121W = np.random.randn(5, 10) # 假设一些随机数据和权重2X = np.random.randn(10, 3)3
+4# 前向传播5D = W.dot(X) # D = WX6
+7# 假设我们得到了D的梯度8dD = np.random.randn(*D.shape) # 和D一样的尺寸9
+10# 反向传播11dW = dD.dot(X.T) #.T就是对矩阵进行转置12dX = W.T.dot(dD)而问题的关键在于矩阵的求导运算。
这里记录一下我目前的计算方法,可能并不是最简单的,但是至少我这个方法是本质的、通用的。也就是用多元函数的链式求导法则,进行计算。
问题
已知Y=WX,Y的梯度dY(即损失函数
结论:
证明:
已知:
求:
由多元函数链式法则:
同理可以算出其他值,整理即得结论
五、神经网络
接下来是关于神经网络(neural network)的学习。本章体量较大,大体思路为:神经网络的建模与结构,数据的预处理、正则化和损失函数,神经网络的动态部分(即神经网络学习参数和搜索最优超参数的过程),以及卷积神经网络。
1. 神经网络的建模与结构
1.1 与神经元的类比
先介绍神经元(neuron or unit)模型。在这个模型中,神经元接受到来自n个其他神经元传递过来的输入信号
这如同:树突将信号传递到细胞体,信号在细胞体中相加,如果最终之和高于某个阈值,那么神经元将会激活,向其轴突输出一个峰值信号。当然这只是一厢情愿的类比,真实的神经元复杂多了。
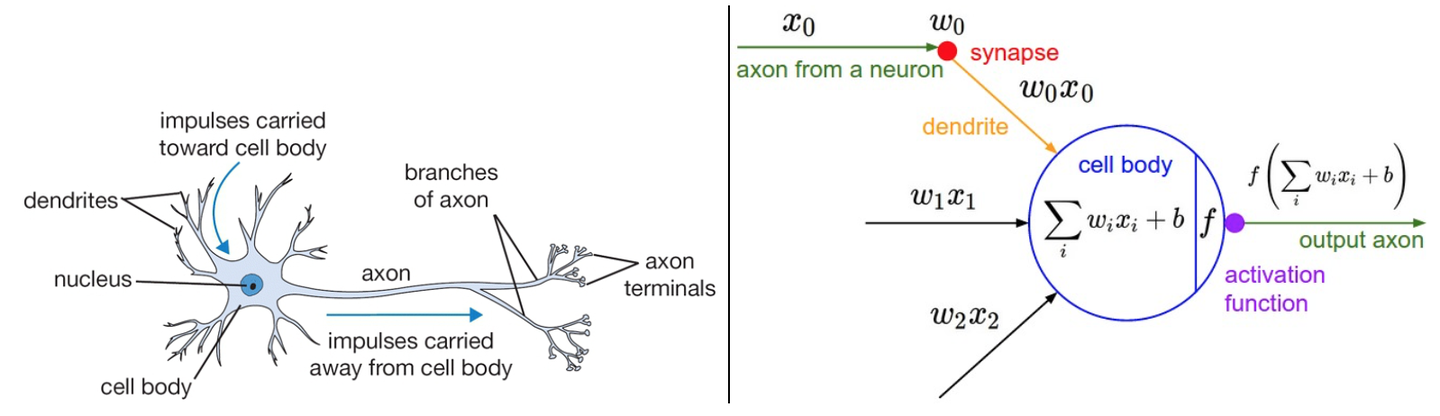
1.2 激活函数
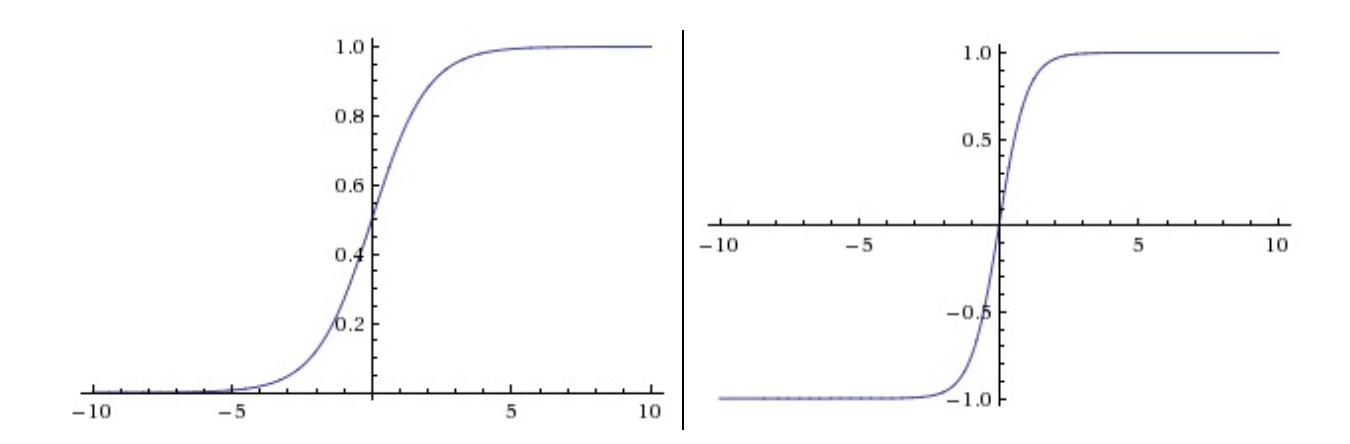
Sigmoid。sigmoid函数就是
Sigmoid函数饱和使梯度消失。也就是说函数值在接近0或1处时梯度几乎为0。在反向传播的时候,sigmoid门的局部梯度若为0,那么与上游梯度相乘的结果也会接近0,这样几乎就没有梯度信号向前传递了。为了防止饱和,必须对于权重矩阵初始化特别留意。比如,如果初始化权重过大,那么大多数神经元将会饱和,导致网络几乎不学习了。
Sigmoid函数的输出不是零中心的。由于sigmoid函数输出永远为正数,那么下一层的神经元输入的数据
记某神经元输出
exp()是计算昂贵的。相对其他激活函数计算时间较长。
Tanh。
ReLU。ReLU即校正线性单元(Rectified Linear Unit)。其函数公式是
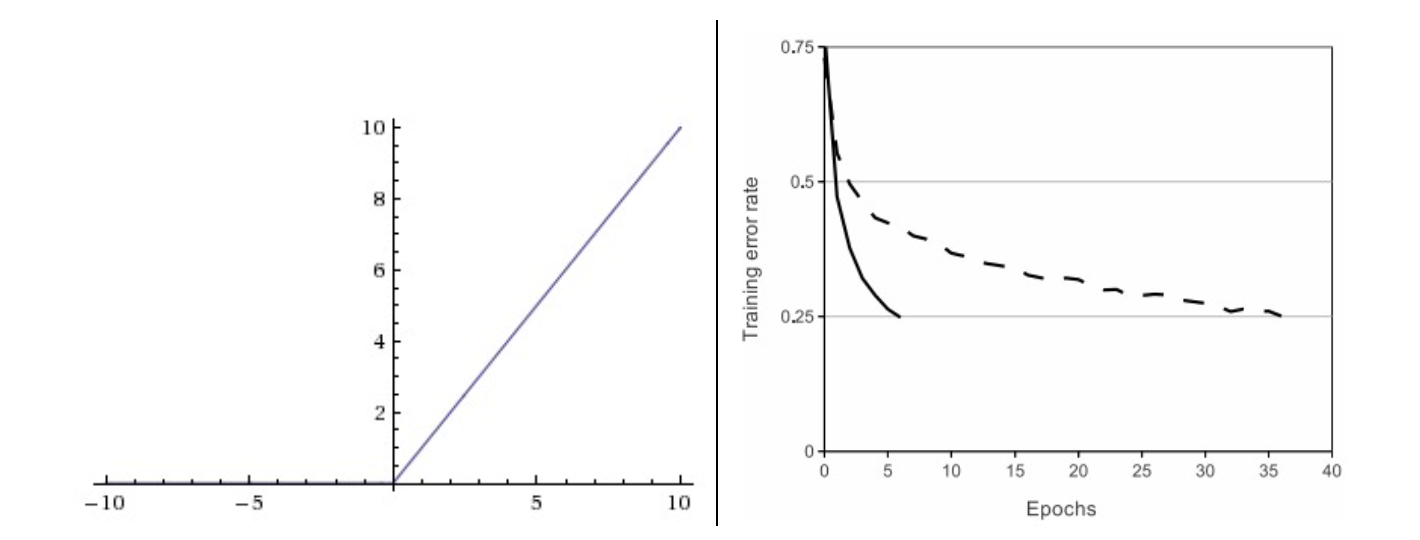
ReLU具有以下优缺点:
- 优点:相较于sigmoid和tanh函数,ReLU对于随机梯度下降的收敛有巨大的加速作用(上图右)。据称这是由它的线性,非饱和的公式导致的。
- 优点:sigmoid和tanh神经元含有指数运算等耗费计算资源的操作,而ReLU可以简单地通过对一个矩阵进行阈值计算得到(把小于0的值设置为0)。
- 缺点:ReLU函数输出不是零中心的。也会产生所谓的z字形下降,当然采用minibatch后就可以一定程度解决这个问题。
- 缺点:“ReLU死亡”——该神经元无法被再次激活,也就是该神经元的输出永远是0,流过的梯度也便成0. 试图解释如下:若一个神经元中
ReLU的变种。为解决“ReLU死亡”问题,人们提出了许多类似ReLU的激活函数。下面列举一些:
Leaky ReLU。
PReLU(P stands for parametric)。
ELU(exponential linear unit)。函数为:(默认
总结:使用ReLU,设置好学习率,或许可以监控你的网络中死亡的神经元占的比例。如果单元死亡问题困扰你,就试试Leaky ReLU或者Maxout,不要再用sigmoid和tanh了。ReLU的变种其实表现和ReLU差不多的,提升1%的正确率已经了不起了,甚至还可能表现更糟糕一点。
1.3 结构
对于普通神经网络,最普通的层的类型是全连接层(fully-connected layer)。全连接层中的神经元与其前后两层的神经元是完全成对连接的,但是在同一个全连接层内的神经元之间没有连接。只有隐层需要激活函数,输入输出层不需要。下面是两个神经网络的图例,都使用的全连接层:
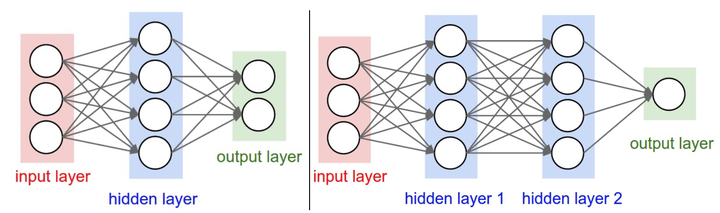
命名规则:当我们说N层神经网络的时候,我们没有把输入层算入。所以上图左边是一个两层神经网络,上图右是一个三层的神经网络。输入层、隐层、输出层。
确定网络尺寸。用来度量神经网络的尺寸的标准主要有两个:一个是神经元的个数,另一个是参数的个数,用上面图示的两个网络举例:
- 第一个网络有4+2=6个神经元(输入层不算),[3x4]+[4x2]=20个权重,还有4+2=6个偏置,共26个可学习的参数。
- 第二个网络有4+4+1=9个神经元,[3x4]+[4x4]+[4x1]=32个权重,4+4+1=9个偏置,共41个可学习的参数。
python代码:
xxxxxxxxxx61# 上图右图例子:2f = lambda x: 1.0/(1.0 + np.exp(-x)) # 激活函数(用的sigmoid)3x = np.random.randn(3, 1) # 含3个数字的随机输入向量(3x1)4h1 = f(np.dot(W1, x) + b1) # 计算第一个隐层的激活数据(4x1)5h2 = f(np.dot(W2, h1) + b2) # 计算第二个隐层的激活数据(4x1)6out = np.dot(W3, h2) + b3 # 神经元输出(1x1)全连接层的前向传播一般就是先进行一个矩阵乘法,然后加上偏置并运用激活函数。
1.4 表达能力
这里不加证明地给出:具有一个隐层的神经网络就可以任意精度地近似一个连续函数。既然一个隐层就能近似任何函数,那为什么还要构建更多层来将网络做得更深?答案是:虽然一个2层网络在数学理论上能完美地近似所有连续函数,但在实际操作中效果相对较差。
另外,在实践中3层的神经网络会比2层的表现好,然而继续加深(做到4,5,6层)很少有太大帮助。卷积神经网络的情况却不同,在卷积神经网络中,对于一个良好的识别系统来说,深度是一个极端重要的因素(比如几十个可学习的层)。对于该现象的一种解释观点是:因为图像拥有层次化结构(比如脸是由眼睛等组成,眼睛又是由边缘组成),所以多层处理对于这种数据就有直观意义。
设置层的数量和尺寸
首先,要知道当我们增加层的数量和尺寸时,网络的容量上升了。即神经元们可以合作表达许多复杂函数,所以表达函数的空间增加。例如,如果有一个在二维平面上的二分类问题。我们可以训练3个不同的神经网络,每个网络都只有一个隐层,但是每层的神经元数目不同:
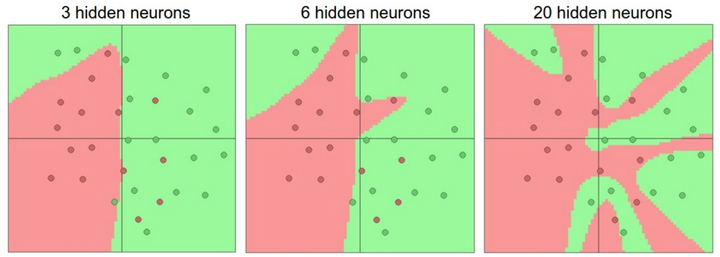
在上图中,可以看见有更多神经元的神经网络可以表达更复杂的函数。然而这既是优势也是不足,优势是可以分类更复杂的数据,不足是可能造成对训练数据的过拟合(overfitting)。而有3个神经元的模型的表达能力只能用比较宽泛的方式去分类数据。它将数据看做是两个大块,并把个别在绿色区域内的红色点看做噪声。在实际中,这样可以在测试数据中获得更好的泛化(generalization)能力。
基于上面的讨论,看起来如果数据不是足够复杂,则似乎小一点的网络更好,因为可以防止过拟合。然而并非如此,防止神经网络的过拟合有很多方法(L2正则化,dropout和输入噪音等),后面会详细讨论。在实践中,使用这些方法来控制过拟合比减少网络神经元数目要好得多。下图中,每个神经网络都有20个隐层神经元,但是随着正则化强度增加,它的决策边界变得更加平滑。
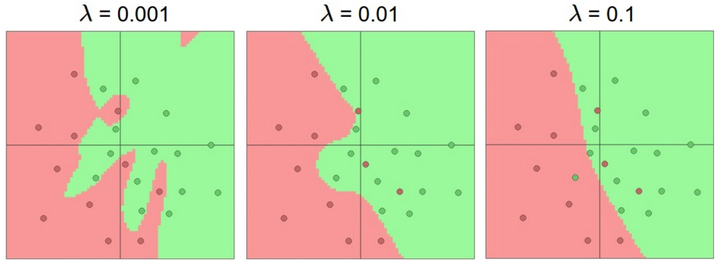
不要减少网络神经元数目的主要原因在于小网络更难使用梯度下降等局部方法来进行训练:虽然小型网络的损失函数的局部极小值更少,也比较容易收敛到这些局部极小值,但是这些极小值一般都很差,损失值很高。相反,大网络拥有更多的局部极小值,但就实际损失值来看,这些局部极小值表现更好,损失更小。
总之,不应该因为害怕出现过拟合而使用小网络。相反,应该进尽可能使用大网络,然后使用正则化技巧来控制过拟合。
2. 数据预处理、正则化和损失函数
2.1 数据预处理
均值减法(Mean subtraction):就是做零中心化(zero-centered)。把数据中每个独立特征减去平均值,从几何上可以理解为在每个维度上都将数据云的中心都迁移到原点,X-=np.mean(X,axis=0)。对于图像来说,我们可以对所有像素都减去一个值,X-=np.mean(X);也可以在3个颜色通道上,分别减去各自的均值。
归一化(Normalization):先对数据做零中心化处理,然后每个维度都除以其标准差,X /= np.std(X, axis=0)。做归一化能使得数据每个维度范围和贡献差不多。由于图像处理中像素的数值范围几乎是一致的(都在0-255之间),所以进行这个额外的预处理步骤并不是很必要。
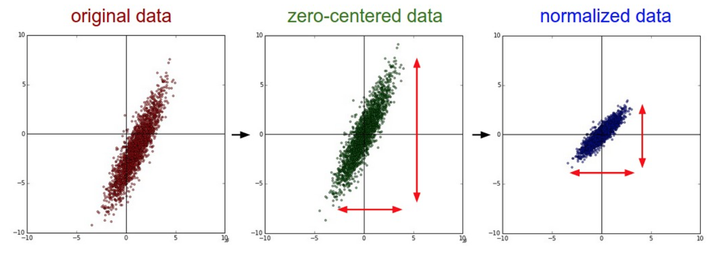
之所以要做零中心化或归一化,课程中这样两个说法。1)输入值有正有负,避免本章1.2节讨论的z字形下降;2)考虑一条过原点的直线划分红蓝两类点(如下图),不中心化的点使得损失值对于直线的抖动更敏感、难以优化。类似的,神经网络某一层的输入均值不为0或者方差不为1,该层网络权重的微小扰动可能会导致该层输出的巨大扰动,从而导致学习困难。

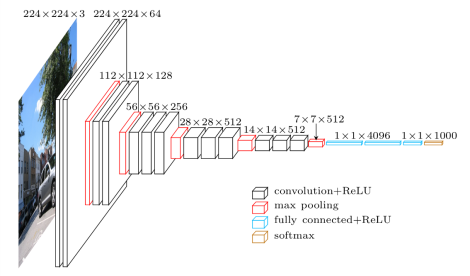
在图像数据预处理时,我们通常只做零中心化处理,有时还会再除以标准差。从训练集中求图片平均值,然后各个集(训练/验证/测试集)中的图像再减去这个平均值。下面是AlexNet、VGG和ResNet如何处理CIFAR-10数据的例子:
- AlexNet: Subtract the mean image (mean image = [32,32,3] array)
- VGG: Subtract per-channel mean (mean along each channel = 3 numbers)
- ResNet: Subtract per-channel mean and Divide by per-channel std (mean along each channel = 3 numbers)
此外,为了介绍的完整性,常见的预处理还有PCA和白化。PCA(principal component analysis,主成分分析)先对数据进行零中心化处理,然后计算协方差矩阵,再对数据协方差矩阵进行奇异值分解,接着将零中心化后的数据投影到特征基准上(去除数据相关性),最后留下了数据中包含最大方差的多个维度,达到降维,从而节省训练时间和存储器空间。白化(whitening)把投影到特征基准上的数据除以该维度的特征值,来对数值范围进行归一化。这里不再深入探究,具体数学细节应该不简单。下图从左到右依次是原数据、去相关性数据和白化后的数据。
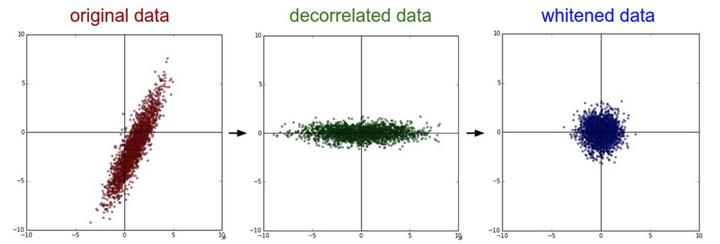
2.2 权重初始化
预处理完数据后,我们还需要初始化所有权重的值。核心目标是:通过合理的初始化权重,让网络在最初的训练过程中能合理地更新权重,而不是直接不学习。下面是几个想法。
全零初始化(错误)。这是一个错误的做法。因为如果网络中的每个神经元都计算出同样的输出,然后它们就会在反向传播中计算出同样的梯度,从而进行同样的参数更新。换句话说,如果权重被初始化为同样的值,神经元之间就失去了不对称性的源头。话是这么说,但是具体举个例子就很麻烦了。自己画了个简单的两层神经网络体会了一下,输入层为x1x2,隐藏层h1h2,输出层y1y2,会发现h1=h2、wx1->h2=wx1->h1、wx2->h1=wx1->h2、wh1->y1=wh2->y1、wh1->y2=wh2->y2(可能有误),反正具有对称性了,显然不是我们想要的。事实上,如果权重只要被初始化为同样的值,不一定要全零,就会产生这样的问题。
小随机数初始化。比如生成一个均值为0,标准差为0.01的正态分布:W = 0.01 * np.random.randn(Din, Dout)。对于浅层网络表现尚可,但是对于较深的网络有问题。下面是六层的神经网络,每层都有4096个神经元,都按照上述正态分布初始化权重,采用tanh激活函数,每层的输出如图:

可见随着深度加深,输出将接近全零的情况,这也会导致权重的梯度接近全零(回忆到反向传播求梯度的过程中,有一项
若初始化分布改成标准差为0.05的正态分布:W = 0.05 * np.random.randn(Din, Dout)。会有以下结果:

可见由于权重初始值太大,大部分激活函数都饱和了。这也使得局部梯度为0,权重梯度为0,网络也不再学习了。
Xavier初始化。使用1/sqrt(n)校准方差,将权重初始化为W = np.random.randn(Din, Dout) / np.sqrt(Din),也就是均值为0、标准差为1/sqrt(Din)的分布,会有以下结果:

这样做的出发点在于想要输出的方差等于输出的方差。考虑
令

由上图可见,随着深度加深,ReLU的输出将越来越集中在0,同样阻碍了学习。对于ReLU,我们可以通过 sqrt(2 / Din)来校准标准差(Kaiming / MSRA initialization),也就是将权重初始化为:W = np.random.randn(Din, Dout) * np.sqrt(2 / Din),得到的每层结果如下:

ResNet的权重初始化。对于卷积层,
2.3 正则化
正则化被用来避免网络过拟合训练数据。之前提及的L1和L2正则化,以及批量归一化(第六章第五节)都是正则化的手段。这里主要是谈论dropout(随机失活)。
dropout的核心想法是在前向传播时,随机设置一些神经元为0,通常可以设置失活概率为0.5。为什么dropout可行,课程中给出两种解释。一是减少神经元之间的共适应关系(co-adaptation),使得在丢失某些特定信息的情况下依然可以从其他信息中学到一些模式,增强鲁棒性。二是通过dropout我们训练了一些共享参数的网络全体。有用就行,我反正不明觉厉。
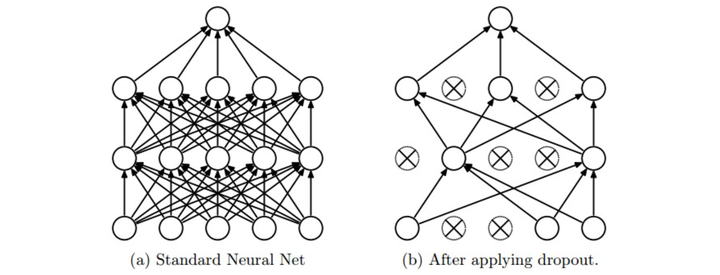
在预测的时候,为了保障对同一个输入的预测结果是确定的,肯定不能进行随即失活。但是我们想要预测时神经元的输出与训练时的预期输出是一致的,否则预测时就不是当初训练的神经网络了。以
xxxxxxxxxx241""" 普通版随机失活: 不推荐实现 (看下面笔记) """2
+3p = 0.5 # 激活神经元的概率. p值更高 = 随机失活更弱4
+5def train_step(X):6 """ X中是输入数据 """7 8 # 3层neural network的前向传播9 H1 = np.maximum(0, np.dot(W1, X) + b1)10 U1 = np.random.rand(*H1.shape) < p # 第一个随机失活mask11 H1 *= U1 # drop!12 H2 = np.maximum(0, np.dot(W2, H1) + b2)13 U2 = np.random.rand(*H2.shape) < p # 第二个随机失活mask14 H2 *= U2 # drop!15 out = np.dot(W3, H2) + b316 17 # 反向传播:计算梯度... (略)18 # 进行参数更新... (略)19 20def predict(X):21 # 前向传播时模型集成22 H1 = np.maximum(0, np.dot(W1, X) + b1) * p # 注意:激活数据要乘以p23 H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # 注意:激活数据要乘以p24 out = np.dot(W3, H2) + b3上述做法有一点小问题,就是在预测时还需要额外增加乘以p的操作,会造成一点性能浪费。不如在训练时除以p,这样预测时就不用乘以p了。有如下代码,称之为反向随机失活(inverted dropout):
xxxxxxxxxx251""" 2反向随机失活: 推荐实现方式.3在训练的时候drop和调整数值范围,测试时不做任何事.4"""5
+6p = 0.5 # 激活神经元的概率. p值更高 = 随机失活更弱7
+8def train_step(X):9 # 3层neural network的前向传播10 H1 = np.maximum(0, np.dot(W1, X) + b1)11 U1 = (np.random.rand(*H1.shape) < p) / p # 第一个随机失活mask. 注意/p!12 H1 *= U1 # drop!13 H2 = np.maximum(0, np.dot(W2, H1) + b2)14 U2 = (np.random.rand(*H2.shape) < p) / p # 第二个随机失活mask. 注意/p!15 H2 *= U2 # drop!16 out = np.dot(W3, H2) + b317
+18 # 反向传播:计算梯度... (略)19 # 进行参数更新... (略)20
+21def predict(X):22 # 前向传播时模型集成23 H1 = np.maximum(0, np.dot(W1, X) + b1) # 不用数值范围调整了24 H2 = np.maximum(0, np.dot(W2, H1) + b2)25 out = np.dot(W3, H2) + b3AlexNet和VGG只在fc6和fc7(两个巨大的全连接层)做了dropout操作,而使用了global average pooling的GoogLeNet和ResNet等根本就不用dropout了。像ResNet只用了BN层和L2正则化。
此外,数据增强(data augmentation)也是很常见的做法。譬如将测试的图片翻转、随机裁剪(random crop)、改变颜色等等做法。对于小数据集,还常见cutout(把照片的一些部分用0代替)、mixup(把两张照片重叠,然后说这是40%的猫,60%的狗)。
正则化的方法很多,这里不一一列举了。
3. 动态部分和训练之后
3.1 学习率策略
下图中给出了学习率大小对损失值更新的直观理解。我们可以从较大的学习率开始学习,并逐渐降低学习率。接下来讨论几种降低学习率的策略。

Learning Rate Decay:Step
在训练一定epoch(代)后(譬如每30代),降低学习率(譬如乘以0.1)。训练多少代、降低多少学习率也是超参数,需要一些尝试与调整。不过也可以采用启发式(heuristic)方案,即观察损失值平滑(plateau)后,降低学习率。

Learning Rate Decay:Cosine
常见的方法。设置学习率
其中
Learning Rate Decay:Linear
常见的方法。设置学习率
Learning Rate Decay:Inverse Sqrt
并不那么常见。设置学习率
其潜在风险在于并没有保持一段时间的高学习率,而是迅速下降了。
当我们设置

Learning Rate Decay:constant
最常见的学习率设定了,也是推荐在你训练网络一开始采用的,可以避免一些不必要的麻烦。
3.2 训练多久?
观察损失值(下左)和正确率(下右)随着训练的变化。右图随着不断的训练会产生过拟合现象,需要在验证集正确率最高的点停止训练。实际操作中,可以设定一个最大epoch大小,然后每一定epoch数后设置检查点,记录下所有参数,最后看哪个检查点具有最高的验证集正确率。

3.3 选取超参数
现在有好多超参数需要设置,有两个直接的方法:
- Grid Search:每个超参数设定几个可能取值,然后一一组合
- Random Search:每个超参数设定一个范围,然后随机从范围中取值
random search可能比grid search更好,出于以下考虑:如果两个超参数一个影响大(下图绿线)、另一个影响小(下图橙线),我们更希望让影响大的超参数取到让绿线最高点的值,而不那么关心影响小的超参数。显然random search更容易找到使得绿线最高的重要超参数的值。

3.4 选取超参数(无大量GPU加持)
3.3节介绍的方法其实在枚举各种超参数组合,耗时耗力。一些基本技巧可以帮助我们选取超参数。
Check initial loss: Turn off weight decay (应该就是令正则化项为0), sanity check loss at initialization. e.g. log(C) for softmax with C classes
Overfit a small sample: Try to train to 100% training accuracy on a small sample of training data (~5-10 minibatches); fiddle with architecture (譬如每层多少神经元), learning rate, weight initialization. Turn off regularization.
Find LR that makes loss go down: Use the architecture from the previous step, use all training data, turn on small weight decay, find a learning rate that makes the loss drop significantly within ~100 iterations. 可以尝试1e-1, 1e-2, 1e-3, 1e-4的学习率。
Coarse grid, train for ~1-5 epochs: Choose a few values of learning rate and weight decay around what worked from Step3, train a few models for ~1-5 epochs. 可以尝试的权重衰减(应该就是正则化项前的
Refine grid, train longer: Pick best models from Step4, train them for longer (~10-20 epochs) without learning rate decay
Look at learning curves: 也就是观察损失值和正确率(训练集和验证集)随着训练的变化
- 一开始损失值不下降,后来突然开始下降——初始化做的不好
- 损失值在较高的时候就平滑了——考虑使用learning rate decay
- 损失值还在下降呢,突然陡然下降一点后就平滑了——过早引入learning rate decay
- 训练集和验证集的正确率都还在不断上升——继续训练!
- 训练集正确率上升且验证集正确率平滑或下降、两者之间的间隔越来越大——过拟合了,考虑增强正则化项、以及获取更多的测试数据
- 训练和验证集中间几乎没有间隔——欠拟合了,考虑训练更久、更大的模型
GOTO step5
最后还有两个建议
- 把每次超参数设定以及相应的learning curves记录下来,提供一个直观的理解
- 梯度比起原值比值可能在1%和0.1%这个量级,太大的话可能说明存在问题
3.5 Model Ensemble
- 独立训练多个模型,测试时取它们结果的平均,可以获得大约2%更佳的预测表现。
- 不是独立训练多个模型,而是取一个模型训练时的多个快照。可以将学习率周期性突然增大再慢慢降低得到模型的多个快照。
- Instead of using actual parameter vector, keep a moving average of the parameter vector and use that at test time (Polyak averaging) 呃没看懂
3.6 迁移学习
很常见的一个方法。迁移学习(transfer learning)简单来说就是拿来一些在大规模数据集上已经预训练(pre-train)好的模型,然后我把输出层外其他层需要学习的参数复制下来,输出层随机初始化,最后做一些微调(fine-tune)工作——可以设置底层的学习率相对较低甚至为零,高层的学习率相对较高,从而对网络进行学习。这样设置学习率是出于越接近底层的泛化能力越高。
微调可以加速收敛,并(有时)能提高正确率(因为预训练模型是在一个更大规模数据集上训练的)。

Distributed Training和Large-Batch Training未整理,反正我们也没有几百个GPU
六、卷积神经网络
事实上课程中卷积神经网络是放在第五章第二节数据预处理、正则化和损失函数之前讲的,但是我的整理遵循了课堂笔记的顺序。于是将卷积神经网络部分放在了如何训练神经网络之后。
本章主要分为两个部分,首先探讨用来构建卷积神经网络的各种层(convolutional layer, pooling layer and normalization layer, fully connected layer),然后探讨现有的卷积神经网络架构(AlexNet, ZFNet, VGG, GoogLeNet, ResNet)。
1. 概述
常规神经网络如第五章1.3节所示,我们先把数据展开成向量,经过几个全连接层后,得到最终的评分。这个方案存在问题:将数据展开成向量会破坏原有的空间结构;需要学习的参数的数量会随着输入尺寸的增加而爆炸(显然的,想想权重的数量)。
卷积神经网络(convolutional neural network)是由层组成的。有以下四种可以构建卷积神经网络的层:
- 卷积层(convolutional layer):用filter(一个张量)划过输入数据,做内积运算,得到新的数据。
- 池化层(pooling layer):downsample数据
- 归一化层(normalization layer):将输入数据做归一化,符合标准正态分布。
- 全连接层(fully connected layer):与之前常规神经网络讨论的一致。
此外卷积层和全连接层对输入执行变换操作的时候,最后会用到激活函数,通常是ReLU。一个简易的卷积神经网络便可由[Conv ReLU Pool]反复叠加而成。下面将讨论卷积层、池化层和归一化层。默认情况下,讨论的例子还是CIFAR-10的数据集。
2. 卷积层
2.1 引入

上图是一个3*5*5的filter,取照片中一块3*5*5的一块数据,与filter(也称作kernel)做没有对核翻转的离散卷积运算(也就是对应位置相乘后再求和,后文多称之为multiply-add操作)得到一个数值,得到的数值还需要再加上偏置b(一个filter一个偏置,是一个数)。易见filter划过整张照片会得到一个1*28*28的输出结果,称之为激活图(activation map)。之所以大小是1*28*28,是因为四周各有两个像素没法算出结果。
例子如下图:(输入3*4的数据,核大小为2*2,输出2*3,输出的每一个元素经历4次multiply-add运算)

2.2 多个filter
进一步,我们采用多个不同的filter,一个输入可以得到更多的激活图;再若一批(batch)里面有多个输入,那么输出会进一步增加:(下图中,C: channel, H: height, W: width, K: kernel)

2.3 加入ReLU
由于卷积层做的是线性运算,两个卷积层如果直接拼在一起,那么我们只会得到另一个卷积层。因此,一般情况下要在卷积层之间加上非线性的激活函数(通常就是ReLU):

2.4 卷积层的filter学到了什么呢?
下面是AlexNet的一个例子:(AlexNet第一个卷积层中用了64个filter,每个filter大小是3*11*11)

可见,filter常常学到oriented edges and opposing colors.
2.5 进一步讨论输出的大小
输出的channel大小等于filter的个数。不妨假设输入和filter都是正方形,输入边长为W,filter边长为K,那么输出的边长为
为了避免输出尺寸缩小,需要在输入中增加padding,通常在输入数据的四周增加P圈0,称之为zero padding。此时输出的边长为
之前默认了filter在输入数据划动的步长(stride)是1,我们可以设置步长为S。那么输出的边长为
2.6 接受域(感受野)
接受域(receptive field)指影响到输出单元的所有输入单元的集合。有的时候接受域只指一个卷积层,输入数据的哪部分影响到输出的一个单元;有的时候指最初的输入照片的哪部分影响到这个输出值了,譬如:

记L是卷积层的层数,K是filter的边长,那么接受域边长是
两层的3 * 3filter的卷积层接受域与一层5 * 5的相同,
Problem: For large images we need many layers for each output to "see" the whole image. Solution: Downsample inside the network. 上面提到的步长和之后要讨论的池化都是downsample的方法。
2.7 Summary

注意到上面说kernel size是
2.8 一道题目

每个filter需要学习的参数个数是3*5*5+1(for bias) = 76, 有10个filter,所以总共要学习参数个数为760.
multiply-add操作就是之前所说的内积。
2.9 其他类型的卷积
目前我们讨论的是2D卷积。此外还有1D和3D的卷积。所谓维度应该可能是指输入数据除去通道维度后剩下的维度数。这里不再展开,只做了解。
3. 池化层
池化层(pooling layer)的作用是降低数据体的空间尺寸(downsample),从而减少网络中参数的数量,使得计算资源耗费变少,也能有效控制过拟合。下面是max pooling的例子:(在2*2的网格内取最大元素,网格移动的步长为2)

有两点值得指出:
- 池化层引入了不变性:即便输入的部分数据稍微改变,经过池化层后输出可能不变。
- 池化层没有任何需要学习的参数
除了max pooling外,常见的还有average pooling。
总结如下:

4. 案例LeNet-5
采取了经典的架构:[Conv,ReLU,Pool] x N, flatten, [FC, ReLU] x M, FC. (flatten是将张量展开成向量,FC是全连接层)。下面是LeNet-5的设计(1998年为解决文字识别而提出的卷积神经网络架构):

(图中Weight Size最前面两个就是filter的大小,后面两个就是全连接层的权重矩阵大小)
表格其实已经体现出所有信息了,要看懂!
5. 归一化层
深网络很难训练,不容易收敛。而归一化层(normalization layer)则能帮助神经网络更快收敛,其中最常见的当属批量归一化(batch normalization,BN)。之所以可行,据说是帮助减少了“internal covariate shift”。在训练过程中,因为各层参数不停在变化,所以每个隐层都会面临covariate shift的问题,也就是在训练过程中,隐层的输入分布老是变来变去,这就是所谓的“Internal Covariate Shift”。于是,我们通过一定规范化手段,把每层输入值的分布强行拉回到均值为0方差为1的标准正态分布,就可以避免“internal covariate shift”了。事实上这还停留在经验层面,没有很多理论上的支持。
先来看看全连接层的批量归一化。

进行一波上图的解释:输入数据有D个维度,一批有N个数据,所以输入是N*D的;
再来看看卷积神经网络的批量归一化。
卷积神经网络每个激活图有一个

其实就是把每个channel(也就是每个激活图)的所有数值去做运算。
此外,需要强调的是训练时和测试时的BN层表现是不一样的。训练时
通常我们把BN层插入到全连接层和卷积层之后,在非线性运算前(譬如tanh激活函数)。
除了批量归一化,我们还有一些其他的归一化手段。如Layer Normalization和Instance Normalization(训练和测试表现一致,不再受同一批其余数据影响):


6. AlexNet

输入227*227;一共八层;5层卷积层;max pooling;3层全连接层;ReLU激活函数;使用"local response normalization",但是目前不用了,也不做介绍;在两个GTX580上训练,由于GTX580只有3GB内存,所以模型要分到两个GPU上训练;激活函数还是采用了ReLU;损失函数使用softmax。具体如下(虽然我怎么感觉下表和上图有点对不上,但是问题不大,关键在于分析过程):

选表格中几个数据分析(memory是指输出的大小,参数是指该层需要学习的参数,flop是指从输入到输出要做多少次floating point operations):
- cov1层输出H/W为56。由公式W’ = (W – K + 2P) / S + 1容易算得
- cov1层memory为784KB。输出张量有64*56*56=200704个元素,每个元素是一个单精度浮点,占4个字节,所以有200704*4/1024=784KB
- cov1层参数个数为23k。每个filter有3*11*11个元素,对应还有一个偏置,一共有64个filter,所以总个数为64*(3*11*11+1)=23296
- cov1层的flop运算有73M次。flop运算就是floating point operations,这里就是multiply-add运算。flop = (number of output elements) * (ops per output elem) = (Cout x H’ x W’) * (Cin x K x K) = (64 * 56 * 56) * (3 * 11 * 11) = 72,855,552
- pool1层输出H/W为27。W’ = floor((W – K) / S + 1) = floor(27.5) = 27。注意到这是除不尽的,需要去尾法舍入
- pool1层memory为182KB。计算方法和cov1层的一致,64 * 27 * 27 * 4 / 1024 = 182.25
- pool1层无需要学习的参数
- pool1层flop运算近似为0次. 事实上为 (Cout x H’ x W’) * (K x K) = (64 * 27 * 27) * (3 * 3) = 0.4M。每个输出的元素都是从K x K的网格中取最大值,这里flop运算指取最大值的运算,而不是之前cov1层的multiply-add运算了。
- fc6层参数37749k个参数(个人觉得更正为37753k)。fc6层输入9216个神经元,输出4096个神经元,所需要参数9216 * 4096 + 4096 = 37752832,注意到这里每个输出神经元还要对应一个偏置。
- fc6层flop运算38M次。fc6层输入9216个神经元,输出4096个神经元,需要9216 * 4096 = 37748736次运算。这里flop运算又变成multiply-add运算了。
关于怎么提出AlexNet这样的架构的,可能是通过大量反复试错(trial and error)得到的。
分析每一层的存储大小、参数个数和flop运算,我们可以画出如下柱状图(具体结论也在图中显示了):

7. ZFNet
其实就是更大的AlexNet,也是采用了5层卷积层,3层全连接层,除了:
- CONV1: change from (11x11 stride 4) to (7x7 stride 2)
- CONV3,4,5: instead of 384, 384, 256 filters use 512, 1024, 512
计算量和存储量都大于AlexNet。
8. VGG
VGG和AlexNet对比如下(VGG应该是画错了,分别少画了一个和两个卷积层。VGG16有13层卷积层和3层全连接层;VGG19有15层卷积层和3层全连接层):

VGG16每层大小具体为(max pooling层的通道数应该是上面标的数字的一半,其实看图片的宽度可以看出来):
VGG的设计遵循以下设计规则:
- All conv are 3X3 stride 1 pad 1
- All max pool are 2X2 stride 2
- After pool, double channels
下面对以上设计规则进行分析
1)All conv are 3X3 stride 1 pad 1
VGG所有卷积层的filter大小都是3*3的,而在AlexNet不同层有不同的filter大小——11 * 11、5 * 5和3 * 3。由本章2.6节可知,两层3 * 3的卷积层和一层5 * 5的卷积层接受域相同,而两层3 * 3只需要更少的需要学习的参数,并且在两层之中加入激活函数,给网络更多非线性元素以及更深的深度。
关于更少的参数。考虑Conv(5x5, C->C)和Conv(3x3, C->C)+Conv(3x3, C->C),其中C->C意味着输入数据是C通道的,输出还是C通道。前者需要25C2个参数、25C2HW次flop运算,而后者一共需要18C2个参数、18C2HW次flop运算。
这样kernel size不再是一个超参数,而是规定好的常数。
2)All max pool are 2X2 stride 2. After pool, double channels
考虑池化前后的卷积层:

可见两者需要的flop次数相同。
关于如何在pool后double channels,应该是通过下一个卷积层实现的,不是通过池化层实现的,这样也会导致有些卷积层的输入和输出通道并不相同。
最后,关于AlexNet和VGG所需要的内存、参数和flop数有下面直观的对比。

最后的最后,由于批量归一化尚未提出,为了使网络收敛,VGG训练时先是训练比较浅的版本,然后再在训练好的层之间插入新的层,继续训练。
9. GoogLeNet
主要讨论几个重要设计思想,核心在于节约且高效。
stem network

通过一些操作先把输入的长宽降到28,注意到VGG也将长宽降到28,而GoogLeNet的所需计算量更小。
Inception Module

要点:不同于VGG将kernel大小设置为3 * 3,GoogLeNet计算了四种不同的kernel size组合;inception module在GoogLeNet中反复出现;采用了1*1卷积层,来减小通道大小。最后这个filter concatenation应该就是简单地把多个激活图按照channel维度拼起来。
Global Average Pooling

回忆到,之前的模型大部分需要学习的参数在全连接层,于是GoogLeNet先用了kernel size等于last conv layer‘s spatial size的average pooling来得到一组神经元,再用一层全连接层得到输出层。
Auxiliary Classifiers

GoogLeNet提出时还没有批量归一化,让网络收敛很困难。于是GoogLeNet在网络两个地方分别增添了一个auxiliary classifier,也是做global average pooling来得到阶段性的评分。在训练时,权重的梯度将根据三个分类器综合得到。
10. ResNet
ResNet(残差神经网络)拥有了BN层的加持,可以训练更深(百层)的网络。但是当网络加深后,会发现深网络在训练和测试的表现可能均不佳,如下图:

这是因为深网络存在underfitting的问题(注意到不是overfitting,否则训练的表现会更好)。按理说深网络有更多表现能力,从而表现得应该至少和浅网络一样好。退一步讲,把浅网络直接复制过来并在最后加上几个恒等层(identity,指该层的输入输出一致),从而构建出和浅网络一样性能的深网络。从这一点出发,我们能不能修改一下网络结构,能帮助网络学习到恒等层,这就是ResNet的一个重要设计思想。
譬如,在两个卷积层的输出结果F(x)上再加上x,当作最终的输出。当两个卷积层的核都设置为0,那么F(x)结果必然是0,那最终结果就是输入,也就是学到了恒等层。这样的一个组件称为residual block,是ResNet的基本组件。

ResNet的基本设计如下图。首先用stem network来减小输入数据的尺寸,然后通过多个stage。每个stage由通道数区分,每个stage又由多个residual block组成,所有residual block的卷积核都是3 * 3大小的。最后通过global average pooling和一层全连接层得到输出层。

在进一步加深ResNet的深度时,研究者又将"basic" residual block全替换为"bottleneck" residual block。设计如下图所示,可以看出flops会略少一点,此外网络会更深一点(每个block有3层):

最后给出五种ResNet设计,以及计算量和ImageNet表现。

关于每个block的ReLU层和BN层有以下两种设计。"pre-activation" ResNet block在测试中有百分之零点几的正确率提升。

11. 其他
在ResNet之后又有更多的架构被提出,如ResNeXt、grouped convolution、squeeze-and-excitation network、densely connected neural network、tiny network(针对移动设备),以及对生成最优网络架构的网络研究(neural architecture search)。
12. 结论
目前不要自己设计神经网络。用ResNet-50或者ResNet-101就行了。如果还想要在移动设备上运行的话,可以看看MobileNets和ShuffleNets。
七、循环神经网络
循环神经网络即RNN(recurrent neural network)能更好地处理序列的信息,即前面的输入和后面的输入是有关系的。细节因具体实现不同而不同,这里只是讲讲我理解的内容。先看一下其简单的结构。
1. 基本结构

其中红色为输入层,绿色为隐藏层,蓝色为输出层。之前讨论的神经网络都是one to one的结构。one to many如image captioning: image->sequence of words; many to one如video classification: sequence of images->label; many to many (特别的有seq2seq结构)如machine translation: sequence of words->sequence of words、per-frame video classification: sequence of words->sequence of labels.
2. vanilla RNN
我们来看一下最简单的RNN实现。

RNN有内部状态,在t时间记为ht(hidden state),且有关系式
于是一个many to many的RNN就长这样:

类似也可以得到one to many, many to one和seq2seq结构。特别的seq2seq结构其实是many to one + one to many:

例子
我们来看一个image captioning的具体例子。

首先将照片经过训练过的CNN网络得到特征向量。特征向量通过一个全连接层得到h0待用。我们用一个词汇表记录每个单词对应一个非负整数,其中还包含有<START>, <END>两个特殊token,分别标记着开始和结束。我的x输入是非负整数向量(因为每个单词对应一个非负整数),但是这样包含的信息就太少了,我们先把x通过一个映射变成浮点数矩阵再进行输入(一个整数对应一个浮点向量,上图没有体现)。
训练时:我们有图像captioning的ground truth值,将GT值作为输入x[t](整数向量),经过映射得到了对应的浮点矩阵,扔入隐层
测试时:将h0和<START>token输入,得到的yi包括了所有单词的得分,找最大的那个作为最终的单词。将单词作为xi+1继续输入,如此往复直到<END>token出现。
vanilla RNN 梯度流问题

之前已经提到,W对所有的tanh都是一样的。这就导致了在反向传播时,乘以大量W,如果W的奇异值大于1,那么导致梯度爆炸,如果奇异值小于1,导致梯度消失。
3. LSTM
LSTM即Long Short Term Memory,可以解决vanilla RNN的梯度问题。

上图中
LSTM内部状态在ht外新增了ct,也就是cell state。它有四个门,分别是:
- i: Input gate, whether to write to cell
- f: Forget gate, whether to erase cell
- o: Output gate, how much to reveal cell
- g: Gate gate (?), how much to write to cell
在反向传播时,不再会产生多次W相乘所带来的梯度问题。
RNN还有很多变种,譬如Gated Recurrent Unit (GRU)。具体细节不再展开。
4. 注意力机制
4.1 Attention
先复习一下seq2seq模型。

上图中编码器的输入序列为x1,...,x4,通过等式
问题在于,当输入序列很长时,最后的context vector c难以记住所有内容。针对此我们提出了attention机制。

同样的,编码器的输入序列为x1,...,x4,通过等式

对于上述操作有直观理解。 Context vector attends to the relevant part of the input sequence “comiendo” = “eating” so maybe a21=a24=0.05, a22=0.1, a23=0.8。
可以看到The decoder doesn’t use the fact that

4.2 Attention Layer
设计是看得懂,但是怎么想出来的暂时搞不懂。

4.3 self-attention
self-attention layer和attention layer几乎一样,除了自注意力层的query输入也是由input vector生成

可以发现虽然Yi是所有输入的函数,但是自注意力机制并没有记录位置信息,Yi就对应Xi。那处理序列肯定是不够的。于是我们还需要引入位置编码(position encoding)。位置编码将位置信息注入到输入里,也就是输入X已经包含了位置信息。具体位置编码这里不展开。
CNN with Self-Attention

4.4 Three Ways of Processing Sequences
如图:

重点:RNN并行度很差;卷积需要很多层才能看到长序列;自注意力一层就可以看到所有序列,但是对于长序列计算复杂度很高(不过可以高度并行)。
4.5 Transformer
transformer由多个transformer block组成,如图

transformer在NLP中表现出色!但是计算量爆炸!
八、Visualizing and Understanding
本章试图探讨CNN不同层到底学到了什么。6.2.4我们已经给出了AlexNet中第一个卷积层filter表示的照片,但更高层的filter都不是三通道了,自然不能表示一个RGB照片。我们可以用灰度表示,但是结果不令人感兴趣。
大部分内容只是讲讲想法,不是很清楚。
有几个想法
对AlexNet的FC7层(一个4096维向量)使用Nearest neighbors分类具有不错的结果,较于直接对原始图片进行Nearest neighbors分类。
对AlexNet的FC7层使用PCA或者更高级的t-SNE降维,将4096维向量降到2维。somehow可以将同一类型的图片放在了一起。http://cs.stanford.edu/people/karpathy/cnnembed/
maximal patches。选取某一层的一个通道,观察不同图片通过网络时,该通道的值。visualize image patches that correspond to maximal activations?
saliency via occlusion(显著性通过遮挡...)。通过遮挡照片的一些部位,然后check how much predicted probabilities change。

saliency via backprop。计算与图像像素对应的正确分类中的标准化分数的梯度,这个梯度告诉我们当像素点发生轻微改变时,正确分类分数变化的幅度。然后可视化这个梯度,可以告诉我们原图哪些像素会大幅度影响判断结果。得到的可视化图称为saliency map。这里的反向传播还有trick:Images come out nicer if you only backprop positive gradients through each ReLU (guided backprop)

gradient ascent:生成一个图片,使某个目标神经元的值最大。对于如何生成比较真实的图片有非常多的研究。

对抗adversarial。挺有意思的想法
- Start from an arbitrary image
- Pick an arbitrary category
- Modify the image (via gradient ascent) to maximize the class score
- Stop when the network is fooled

feature inversion。Given a CNN feature vector for an image, find a new image that: 1) Matches the given feature vector; 2) “looks natural” (image prior regularization)
最后,介绍了deep dream和neural style transfer. 挺有意思的两个东西。

九、Detection、Segmentation
之前讨论的计算机视觉任务只是给一张图片做分类,但是计算机视觉任务远不止于此。

- Classification: 一张图片一个标签
- Semantic Segmentation(语义分割):每个像素一个标签
- Object Detection(目标检测):找到照片中多个物体,并分类
- Instance Segmentation(实例分割):目标检测和语义分割的结合
1. Object Detection
1.1 Task Definition
Input: single RGB image
Output: A set of detected objects; For each object predict:
- Category label (from fixed, known set of categories)
- Bounding box (four numbers: x, y, width, height)
1.2 Challenges
- Multiple outputs: 每张照片输出多个对象
- Multiple types of output: Need to predict "what" (category label) as well as "where" (bounding box)
- Lage images: 更高的分辨率
1.3 Detecting a Single Object
如果照片只有一个对象,我们有如下方案:

即:拿来一个已经预训练好的网络,在原来的损失函数后再增加一个关于Box Coordinates的损失值,继续训练即可。这种多个损失值加权求和得到最终的损失值,我们称为multitask loss. 但是显然一张照片可能不止一个对象,这个简单的方案并不可行。
1.4 Detecting a Multiple Objects
Sliding Window
我们来看一个检测多个对象的想法:Sliding Window。固定一个大小为h*w的窗口,一个一个像素地划过大小为H*W的图片,每次判断这个窗口的内容是狗、猫还是背景。很显然有窗口数目太大的问题。并不可行

Region Proposals
通过一些启发式的手段,在图像上找到可能的区域。其中Selective Search方法可以利用CPU在几秒内找到2000多个区域。具体细节不做了解。
1.5 R-CNN: Region-Based CNN
利用region proposals,我们可以有如下直观做法:

- 原图跑region proposals得到很多区域
- 将这些区域缩放为相同大小
- 扔到CNN,得到分类分数和Bbox。所谓的Bbox就是指对region proposals得到的bounding box的修正(图中有一个修正方案)。
- 在测试时,可以用分类分数来扔掉一些候选区域
这些CNN共享权重。训练的时候,我们通过GT boxes将bounding boxes分成了positive、neutral和negative,然后根据这个分类进行训练。每个positive box又和一个GT box配对,这样就可以训练bounding box transformation了,最后用multitask loss得到损失值。

1.6 Comparing Boxes: Intersection over Union (IoU)
如何评价预测的区域和ground truth之间的相近程度呢?我们有如下的办法:

1.7 Overlapping Boxes: Non-Max Suppression (NMS)
Problem: Object detectors often output many overlapping detections.

上图中,Object detectors找到了四个区域,它们是狗勾的可能性如图所示。可以看到同一只狗勾都有两个区域。如何排除关于同一个物体的多个区域呢,我们有如下Non-Max Suppression算法(一种贪心算法):
- Select next highest-scoring box
- Eliminate lower-scoring boxes with IoU > threshold (e.g. 0.7)
- If any boxes remain, GOTO 1
就是留下不怎么重叠且得分高的框,把与这些框重叠多的框去掉。
然而NMS算法存在一个小问题,考虑下面的图片:

如果一个图片高度重叠,如何做object detection呢。目前没有非常好的方案。
1.8 Evaluating Object Detectors: Mean Average Precision (mAP)
知道如何评价预测的区域和ground truth之间的相近程度后,那我们如何评价一个Object Detector呢?我们采用mean average precision,具体如下:
Run object detector on all test images (with NMS)
For each category, compute Average Precision (AP) = area under Precision vs Recall Curve:
For each detection (highest score to lowest score):
- If it matches some GT (groundtruth) box with IoU > 0.5, mark it as positive and eliminate the GT
- Otherwise mark it as negative
- Plot a point on PR Curve
Average Precision (AP) = area under PR curve
Mean Average Precision (mAP) = average of AP for each category
For “COCO mAP”: Compute mAP@thresh for each IoU threshold (0.5, 0.55, 0.6,…, 0.95) and take average

上图中,0.99、0.95和0.10三个区域分别和三个GT box匹配,0.9和0.5两个区域没有匹配。precision依次为1/1,2/2,2/3,2/4和3/5. recall依次为1/3,2/3,2/3,2/3和3/3.
1.9 Fast R-CNN
再看看1.5节介绍的R-CNN,它的速度相当慢。一张图片就有2000左右个区域,这些区域都要通过CNN。由于这些区域其实高度重叠,导致了太多冗余计算。
fast R-CNN先运行CNN,再进行warp(图像缩放)。如下图所示:

fast R-CNN下大部分的计算都在backbone network里了,per-region network相对轻量。使得高度重叠的区域不会造成过多冗余计算。
下面着重了解一下如何crop(裁剪) features,也就是Region of Interest (Rols) Pool的具体内容。

原图上的候选区域对应特征图(就是原图经过CNN生成的特征图)一块区域。将特征图划分成网格,将得到的对应区域snap(对齐)到网格。再进行max-pool得到固定大小的区域。但是这种对齐手段会:在特征图比原始图片尺寸小的情况下,一点点的精度损失映射到原始图片上就存在很大的像素点差别。于是有进阶版本ROI Align就是取消了snapping的操作,使用双线性内插的方法获得坐标未浮点数的像素点上的图像数值。具体细节不再展开(不过这门课的作业好像需要ROI Align哦,但是cs231n的作业没有R-CNN)。
1.10 Faster R-CNN
Fast R-CNN大部分时间花在了region proposal上。Faster R-CNN使用Region Proposal Network (RPN)来得到候选区域。Faster R-CNN的设计图如下:

- 提取特征:输入固定大小的图片,进过卷积层提取特征图feature maps
- 生成region proposals: 然后经过Region Proposal Networks(RPN)生成region proposals。该层通过softmax判断anchors属于foreground或者background,再利用bounding box 回归修正anchors获得精确的proposals(候选区域)。
- ROI Pooling: 该层的输入是feature maps和proposals,综合这些信息后提取proposal feature maps
- Classification: 将Roi pooling生成的proposal feature maps分别传入softmax分类和bounding box regression获得检测物体类别和检测框最终的精确位置。
重点在于RPN的设计。特征图上设置几个anchor,训练一个小的神经网络判断anchor box是背景还是物体,这个神经网络还要预测box transform来改变anchor box的尺寸。使用K个不同的anchor box大小。。反正很不清楚的我觉得。
上述的方案称做two-stage object detector:
First stage: Run once per image
- backbone network
- region proposal network
Second stage: Run once per region
- crop features: Rol pool / align
- predict object class
- prediction bbox offset
与之对应的还有one-stage object detector,差不多就是在判断anchor box是背景还是物体时,直接判断它是什么具体物体,不需要second stage了。
反正,目前one-stage的表现在逐步赶上two-stage,更深的backbone network表现更好。。。很复杂的一个话题,目前了解大概吧。
2. Semantic Segmentation
2.1 Task Definition
semantic segmentation(语义分割)即:给照片的每个像素打上标签,不区分实例,只关心像素点。譬如下图两头牛不区分哪些像素属于哪头的。

2.2 Sliding Window
用一个滑动窗口遍历整个图片,每次给窗口的中心像素分类(通过CNN)。很直接的方法,但是十分低效。
2.3 Fully Convolutional Network
使用多个卷积层,将原始3*H*W大小的图片,变成C*H*W大小的scores,其中C代表分类的个数,也就是每个像素对每个分类有一个得分,总共有C个得分。最后取最大的那个得分作为该像素的分类。

然而我们知道卷积层往往会做downsample的工作,也就是输出的长宽会比输入小。而我们上面的方案要求最终的scores矩阵的长宽和最初的输入图像相同。我们确实可以使用padding来让卷积层的输出长宽大小不变,但是一直保持长宽大小不变使得计算成本上升。这里我们就需要引入upsample的概念,让输出的长宽比输入大。FCN如下图:

downsample有pooling,那么upsample就有unpooling。unpooling的几种方法:
- Bed of Nails
- Nearest Neighbor

- Bilinear Interpolation
- Bicubic Interpolation
- Max Unpooling

上述unpooling方法都没有需要学习的参数。
downsample有卷积,那么upsample就有transposed convolution(转置卷积)。如下图所示:

然而为什么上述称为转置卷积呢?和转置的关系是什么?下面试图解释。
考虑一维卷积的例子。输入向量

如果我们把矩阵X转置后乘a,就有上图右的结果。这实际上就是转置卷积的结果。个人认为应该是现有上面转置卷积的方法,然后再有这个名字的。
3. Instance Segmentation
3.1 Task Defination
在明确定义前,需要明确things和stuff的概念。
- Things: Object categories that can be separated into onject instances (e.g. cats, cars, person)
- Stuff: Object categories that cannot be separated into instances (e.g. sky, grass, water, trees)
之前讲的object detection就是只给出things,而语义分割则给出things和stuff。
于是实例分割就是指:Detect all objects in the image and identify the pixels that belong to each object (only things!)

3.2 Mask R-CNN
想法也很直接,我们先做object detection,然后再predict a segmentation mask for each object。所谓的mask,我目前认为就是下面这种黑黑的东西:

整个网络只用在R-CNN最后加上一个小CNN预测mask就好了。Mask R-CNN结构如下图:

4. Beyond Instance Segmentation
实例分割又可以引申出好多计算机视觉任务。这里做一个简单的介绍。
panoptic segmentation: Label all pixels in the image (both things and stuff); For "things" categories also separate into instances

human keypoints: Represent the pose of a human by locating a set of keypoints.

dense captioning: Predict a caption per region

3D shape prediction: 下一章内容
十、3D Vision
这里只介绍两个3D视觉任务:
- 从原图预测3D图形
- 从3D图形得到分类
1. 3D Shape Representation
1.1 Depth Map
For each pixel, depth map gives distance from the camera to the object in the world at that pixel. RGB image + Depth image = RGB-D image (2.5D). 之所以称为伪3D,是因为Depth map并不可以给出物体被遮挡部分的数据。获取depth map比较简单,只需要通过一些特殊的3D传感器就行了。

Predicting Depth Maps
即如何从原图预测depth maps,可以通过Fully Convolutional network。损失函数采用L2 Distance比较预测图片和ground truth图片每个像素差距,这是不可行的。这是因为通过一张图片,我们无法分辨远处的大物体和近处的小物体,它们在照片上可能是一样大的。正确的做法是采用Scale invariant loss function(如果所有预测的深度和ground truth有一个倍数差,那么loss认为0),具体函数如下:

Surface Normals
For each pixel, surface normals give a vector giving the normal vector (法向量) to the object in the world for that pixel. 下图中不同颜色表示了不同方向的法向量。

同样用FCN进行预测,损失函数用预测法向量和ground truth法向量的夹角就可。同样我们也是没法给出物体被遮挡部分的数据。
1.2 Voxel Grid
Voxel(体素)就是3D空间的像素。Voxel Grid即: represent a shape with a V*V*V grid of occupancies. 优势:简单。劣势:如果想要精致地捕捉图像,需要更多的小voxel。

Voxel Grid -> Label
先用3D卷积层,再flatten,最后用全连接层得到class scores。此时Voxel Grid表示为一个四维张量,其中第四维为1(即1*V*V*V),我们可以通过元素值为1或者0来表示该位置有没有方块。之所以要第四维,是因为3D卷积的要求。
Input image -> Voxel Grid
- 法一:先2D卷积,再flatten通过一些全连接层,接着reshape为四维张量,通过3D卷积层(需要一些upsampling,因为全连接层得到的3D feature大小比较小),得到Voxel grid。劣势在于3D卷积计算昂贵。
- 法二:可能已经注意到,其实voxel grid只需要3维张量就可以表示了。那我们就全用2D卷积层就好了,特别的最后一个卷积层需要使用V个filter,才能生成V*V*V的3维张量。2D卷积层比3D卷积层计算便宜的同时,也失去了第三维的一些相关性。
Scaling Voxels
注意到,Voxel Grid所占的内存空间是巨大的,譬如一个10243大小、数据类型为float32的Voxel Grid就要4GB内存。有一些小技巧来缩小voxel grid所用的内存空间。
Oct-trees: 使用不同大小的Voxel来组成物体的不同部分。如下图:

Nested Shape Layers:

1.3 Implicit Surface
似乎是用一个隐函数来表示物体表面。这个隐函数就是神经网络。我输入一个三维坐标,这个神经网络告诉我这个坐标在物体里还是物体外。更多细节不讨论。
1.4 Pointcloud

优点:Can represent fine structures without huge numbers of points
缺点:点是无限小的东西,所以pointcloud并没有显式地表现出物体。如果我们想要表示出物体的话,需要将这些点放大。
Pointcloud -> Label

Input image -> Pointcloud(课堂上skip了)

Loss Function
Chamfer distance
对于所有的蓝色点,找到其最近的橙色点,计算它们的距离,并求和。对于所有的橙色点,找到其最近的蓝色点,计算它们的距离,并求和。两个和相加即为最终的损失值。

1.5 Mesh
即:用一组三角形来表示3D shape。如下图:

优点:可以表示多种图形;在节点添加数据,可以给表面上色、增加材质等等。
缺点:Nontrivial to process with neural nets
Pixel2Mesh
即:输入照片,输出mesh。如下图:

下面介绍四个key ideas
Iterative mesh refinement: Start from initial ellipsoid mesh; Network predicts offsets for each vertex
Graph Convolution: 大体就是每个顶点新的值依赖于之前值和周围顶点值的加权。在mesh deformation中我们需要做图卷积。
Vertex Aligned-Features:

Loss Function:
一个正方形可以由两个大三角形表示,也可以由四个小三角形表示。我们应当认为这两种表示方法都是正确的。把mesh转换为pointcloud,然后用chamfer loss function。

2. Metrics
就是如何比较预测值和ground truth之间的接近程度。

3. Camera Systems
就是输入的物品视角是正视的(canonical coordinate)还是随意的(view coordinate)。反正view coordinate泛化更好,测试正确性更高;canonical coordinate数据更容易导入,训练时容易过拟合。
4. Datasets
- ShapeNet:建模的图片
- Pix3D:宜家的家具图
最后讲了讲mesh R-CNN,差不多就是在mask R-CNN的基础上,将物品生成mesh。它似乎不再是通过Ellipsoid Mesh(Pixel2Mesh采用)生成最终的mesh,而是先做voxel grid,再生成mesh。
十一、Videos
视频可以被表示为一个四维张量:T*3*H*W (or 3*T*H*W). 其中T是时间维度。视频分类的主要任务是识别动作,譬如跑、跳、吃等动作。视频往往大小过大,于是在训练时我们使用帧数低的片段,在测试时使用原始视频的片段。如下图:

下面给出几种神经网络方案。
1. Single-Frame CNN
对每帧分别扔到CNN中,最后将每帧的分类分数平均一下,得到最终的分类结果。虽然这种方案丢失了每帧之间联系的信息,但是却表现尚可,可以作为视频分类的基准。

2. Late Fusion
有两种方案
with FC layers

with pooling

之所以称为late fusion是因为每帧图片先各自通过CNN,再扔到一起。虽然有一点学习每帧之间联系的味道,但是味道不浓,目测还是难以捕捉到low-level motion between frames。
3. Early Fusion
把时间维度并到通道维度里,也就是把T*3*H*W的张量reshape成3T*H*W. 然后扔到2D CNN中。看上去可以较好学习每帧之间的联系。但是把时间维度并到通道维度挺aggressive的。进一步说这种操作是No temporal shift-invariance的,因为filters extend over the entire length in time, then if we want to detect changes in color at different times, we need to learn separate filters. (2时刻从蓝色转变为橙色,3时刻从蓝色转变为橙色,就需要两个不同的filter,而3D CNN只需要一个filter就行了,因为这个filter本身就会在时间轴上遍历一遍)

4. 3D CNN (Slow Fusion)
也就是直接用3D CNN就行了。

之所以称为slow fusion是因为receptive field的时间维度是随着时间慢慢增加的。

C3D: The VGG of 3D CNNs
采用VGG的设计理念,把其中的2D CNN改成3D CNN就可以了。表现不错,但是计算量爆炸。
5. Two-Stream Networks
two-stream network使用了像素的运动信息。
Measuring Motion: Optical Flow
光流的具体计算我们不关心,只需只要光流给出像素的运动信息。

Separating Motion and Appearance: Two-Stream Networks
two-stream分别指spatial stream和temporal stream。temporal stream采用了early fusion的方法。表现比之前的方法更好。

6. Modeling long-term temporal structure
So far all our temporal CNNs only model local motion between frames in very short clips of ~2-5 seconds. What about long-term structure?
CNN+RNN
可以预先训练好CNN网络,把CNN当作特征提取器,也就是反向传播时不再更改CNN的值。

Recurrent Convolutional Network
就是把之前的RNN中的矩阵乘法改成卷积

Spatio-Temporal Self-Attention (Nonlocal Block)
即:把第七章的4.3节的2D卷积改成3D卷积。

最后把这些nonlocal block通过3D卷积层连起来就好了
Inflating 2D Networks to 3D (I3D)
想法是把现有的2D CNN架构,修改成3D的。稍微具体来说:
- Replace each 2D Kh x Kw conv/pool layer with a 3D Kt x Kh x Kw version
- Can use weights of 2D conv to initialize 3D conv: copy Kt times in space and divide by Kt. This gives the same result as 2D conv given “constant” video input
十二、生成模型
1. Supervised vs Unsupervised Learning
之前我们讨论的所有内容都归于监督学习(supervised learning)。监督学习和无监督学习(unsupervised learning)的区别如下:

2. Discriminative vs Generative Models
可以通过学习到的概率分布的不同,将模型分成判别模型(discriminative model)和生成模型(generative model)。
Discriminative Model: Learn a probability distribution p(y|x). 输入照片x,输出标签的概率分布。没法处理不合理的输入,譬如下面的网络只学过狗勾和猫猫,现在输入一个猴子,它还是会输出狗勾和猫猫的概率。我们之前讨论的所有内容都是判别模型。

Generative Model: Learn a probability distribution p(x)。生成模型输出照片x,这些照片满足了某种概率分布。生成模型需要对照片有深层次的理解,我生成的狗勾是站着呢还是坐着呢,会不会有三头六臂的猴子呢。
Conditional Generative Model: Learn a probability distribution p(x|y)。条件生成模型可以输入标签,输出可能的照片,这个照片满足标签条件下的概率分布。使用贝叶斯公式就可以从判别模型和生成模型转变成条件生成模型。

3. 分类
通过模型是否能计算p(x)、计算值是不是精确值可以将生成模型分类。我们本章只讨论三个生成模型。

4. Autoregressive Models
Goal: Write down an explicit function for
Input: 输入样本
Loss Function: 采用最大似然估计(maximum likelihood estimation)即最优的权重矩阵W满足:

(回忆最大似然估计,存在即合理,想让采样的样本呈现的概率最大)
Model
通过贝叶斯公式可以将p(x)写成:(x是一张照片的话,那么xi就可以是一个像素)

可以看到p(x)的展开式和RNN的结构十分相似。
PixelRNN

可以看到所有的点都和左边和上边的点相关联。softmax over [0,1,...,255]似乎是指先把所有像素做softmax(注意到softmax范围是0~1),再乘以255.
PixelCNN

PixelCNN比PixelRNN快一点,因为它不是一个像素一个像素算的。但是两个网络都是要顺序执行,都很慢。
它们生成的图片远处看看像是张图片,仔细看看什么都不是。
5. (Regular, non-variational) Autoencoders
在看变分自编码器(variational autoencoder, VAE)之前,我们先看非变分自编码器,也就是常规的自编码器(autoencoder, AE)。自编码器是一种无监督学习模型,希望从输入数据

训练完后,把decoder扔掉,encoder可以用来初始化一些监督学习模型。
不过自编码器只是提取特征,我们也不是很清楚这些特征意味着什么,也没法生成新的图片。在实际操作中,自编码器表现的并不是那么好。
6. Variational Autoencoders
并不能很好的理解这节内容,下面的整理可能有所纰漏
变分自编码器引入了概率,我们一方面可以从原始数据

如何训练这个模型呢?基本思想是想要最大化训练数据的可能性(最大似然)。于是我们需要计算出输入数据x的概率分布
另一个想法是通过贝叶斯公式:
同样我们可以计算

其实我没理解
更具体来说:
首先用贝叶斯公式有:

两边同时对z求条件数学期望(z满足

注意到上面计算用到了一个数学事实:
此外还用到了KL散度的数学定义。
上述结果中有

其实我们上述的做法就是所谓的变分推断(variational inference),求的下界称为变分下界(variational lower bound)。目前有点不明觉厉。反正我们现在要训练encoder和decoder两个网络,使得这个变分下界最大。
那这两个网络具体长什么样呢?这里给出一个例子:

具体训练过程为:

先把输入数据x扔到encoder里得到latent code z在x下的条件分布
变分下界中,蓝色框希望latent code包含足够多的信息来重建data,绿色框则希望latent code不复杂,尽可能接近标准正态。
应用
- 生成图片
- 修改latent code,可以看到不同维对生成数据的影响。譬如一张大头照,人微笑的程度、面对的方向。
反正上述工作生成的图片比较模糊,不过速度挺快的。
7. GAN
GAN即generative adversarial networks(生成对抗网络)。GAN由辨别器(discriminator,D)和生成器(generator,G)组成。生成器G输入latent变量z,生成一张图片。辨别器D则判断输入的照片是真实的还是生成的。生成器的目标是尽可能愚弄辨别器,辨别器的目标是尽可能分辨照片的真假。当然我们的最终目标是得到一个以假乱真的生成器,它生成的图像满足的概率分布
我们共同训练生成器G和辨别器D,目标函数是:
辨别器希望对所有真实数据输出1、对所有伪造数据输出0;生成器希望完全愚弄辨别器,也就是对于伪造数据,辨别器也输出1。这些都在目标函数的minmax体现了。
将目标函数记作V(G,D),那么有如下梯度更新策略:

看上去训练挺简单,但事实上最初版本的GAN相当难训练,我们很难知道什么时候训练结束。打个比方,现在有一个造假币的和一个警察。如果警察侦察技术太高,造假币的还没能更新技术就被抓走了;如果造假币的技术太高,警察都不会发现有假币,造假币的也就会不思进取;唯有两者相辅相成,才能互相促进,我们才会有完美的造假技术。
接下来,我们想证明当

第一个等号是做了还原,第二个等号是把期望写成定义式且把max放到积分号里面。通过令导数为0,得到辨别器

将

先后使用KL散度的定义和JS散度的定义,将等式改写。再根据JS散度的性质得证。
当下基于GAN的网络生成图像的表现非常非常好,关于GAN的论文也成千上万。
十三、强化学习
我们已经讨论过了监督学习和无监督学习,这章我们讨论强化学习(reinforcement learning)的一些基本内容。强化学习的简单定义和目标如下:

1. What is reinforcement learning

在t时刻,agent看到了state st,st可能是噪音或者不完整的;当agent得到状态后,执行action at;最后environment再通过reward rt告诉agent它表现的怎么样。action会导致environment的变化,agent也会根据它看到的state和收到的reward来不断学习。
举两个例子


Reinforcement Learning vs Supervised Learning
如果把state看作input、action看作prediction、reward看作loss,似乎强化学习和监督学习就一样了。但事实上两者有以下本质上的不同:
- Stochasticity:agent获得的state和reward可能是noisy或者incomplete的。强化学习在不同时刻即便看到了相同的状态和做出了相同的action,reward却可能是不同的。
- Credit assignment: 强化学习中reward rt不一定对应着t时刻的动作,可能是之前时刻的某个动作。
- Nondifferentiable: can’t compute drt /dat 因为我们没有environment的模型
- Nonstationary: agent看到的state依赖于之前做的action,随着agent不断的学习,environment可能会暴露更多部分给agent。
2. Q Learning
马尔可夫决策过程(MDP)强化学习中常见的一种数学形式。考虑一个tuple (S,A,R,P,
- S: Set of possible states
- A: Set of possible actions
- R: Distribution of reward 在given (state, action) pair 之后
- P: Transition probability: distribution over next state 在given (state, action) 之后
- γ: Discount factor (tradeoff between future and present rewards)
之所以称这个tuple是MDP,是因为它满足马尔可夫性质(Markov property):The current state completely characterizes the state of the world. Rewards and next states depend only on current state, not history. 现实中常见的例子如走迷宫,我们在一个分叉路口的决策(朝哪个方向走)会导致环境的变化,反应为位置的更新。但新的位置只取决于当前位置和当前走的方向,与之前几步毫无关联(即如何来到当前位置不影响下一步的环境)。
Goal
agent根据policy
具体有:

Finding Optimal Policies
模型具有太多随机性(譬如最初状态,状态转变的可能性,奖励等),所以我们需要找的

Value Function and Q Function

Q函数就是初始状态为s、初始动作为a、采用
Bellman Equation

Optimal Q-function是采用了最佳的策略
下面不加证明的给出两个事实:

于是就有Deep Q-Learning(用深度神经网络来模拟Q函数)

譬如之前的第一节的Atari games,我们有如下的神经网络:(4个action对应着上下左右四个动作)

3. Policy Gradients
已经在数学中迷失了自我




最后一堂课是总结与展望,无整理


 -
- 
 -
-  +
+ 