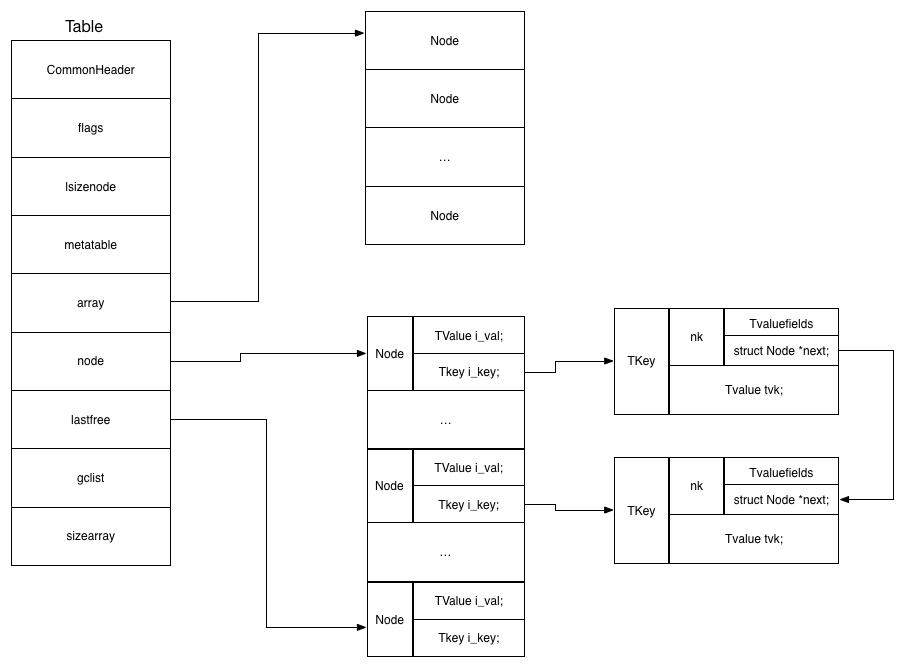
表可以说是Lua中唯一的数据类型了,使用Lua表,可以模拟出其他各种数据结构--数组,链表,树等等.首先来看Lua表的数据类型定义:
(lobject.h)
319 /*
320 ** Tables
321 */
322
323 typedef union TKey {
324 struct {
325 TValuefields;
326 struct Node *next; /* for chaining */
327 } nk;
328 TValue tvk;
329 } TKey;
330
331
332 typedef struct Node {
333 TValue i_val;
334 TKey i_key;
335 } Node;
336
337
338 typedef struct Table {
339 CommonHeader;
340 lu_byte flags; /* 1<<p means tagmethod(p) is not present */
341 lu_byte lsizenode; /* log2 of size of `node' array */
342 struct Table *metatable;
343 TValue *array; /* array part */
344 Node *node;
345 Node *lastfree; /* any free position is before this position */
346 GCObject *gclist;
347 int sizearray; /* size of `array' array */
348 } Table;
来逐个解释一下Table这个数据结构中的成员定义:
在前面的通用数据类型中已经做过解释.
这是一个byte类型的数据,用于表示在这个表中提供了哪些meta method.在最开始,这个flags是空的,也就是为0,当查找了一次之后,如果该表中存在某个meta method,那么将该meta method对应的flag bit置为1,这样下一次查找时只需要比较这个bit就可以知道了.每个meta method对应的bit定义在ltm.h文件中:
(ltm.h)
14 /*
15 * WARNING: if you change the order of this enumeration,
16 * grep "ORDER TM"
17 */
18 typedef enum {
19 TM_INDEX,
20 TM_NEWINDEX,
21 TM_GC,
22 TM_MODE,
23 TM_EQ, /* last tag method with `fast' access */
24 TM_ADD,
25 TM_SUB,
26 TM_MUL,
27 TM_DIV,
28 TM_MOD,
29 TM_POW,
30 TM_UNM,
31 TM_LEN,
32 TM_LT,
33 TM_LE,
34 TM_CONCAT,
35 TM_CALL,
36 TM_N /* number of elements in the enum */
37 } TMS;
该Lua表Hash桶大小的log2值,同时有此可知,Hash桶数组大小一定是2的次方,即如果Hash桶数组要扩展的话,也是以每次在原大小基础上乘以2的形式扩展.
存放该Lua表的meta表,这在后面再做讲解.
指向该Lua表的数组部分起始位置的指针.
指向该Lua表的Hash桶数组起始位置的指针.
指向该Lua表Hash桶数组的最后位置的指针.
GC相关的链表,在后面GC部分再回过头来讲解相关的内存.
Lua表数组部分的大小.
这里注意一个细节,lsizenode使用的是byte类型,而sizearray使用的是int类型.由于在Lua的Hash桶部分,每个Hash值相同的数据,会以链表的形式串起来在该Hash桶中,所以即使数量用完了也不要紧.因此这里使用byte类型,而且是原数据的log2值,因为要根据这个值还原回原来的真实数据,也只是需要移位操作罢了,速度很快.这个细节中可以看到,在Lua的内存使用方面,还是扣了不少细节的地方.
紧跟着来看看Lua表中结点的数据类型.首先从Node的类型定义可以看出,它包含两个成员,其中一个表示结点的key,另一个表示结点的value.值部分就不多解释了,还是Lua中的通用数据类型TValue,来看看key部分的含义:
(lobject.h)
329 typedef union TKey {
330 struct {
331 TValuefields;
332 struct Node *next; /* for chaining */
333 } nk;
334 TValue tvk;
335 } TKey;
可以看到这个数据类型是一个union类型,一般看到一个数据类型是union,就可以知道这个数据想以一种较为省内存的方式来表示多种用途含义,而这些用途之间是"互斥"的,也就是说,在某个时刻该数据类型只会有其中的一个含义.这种C编程技巧在Lua中非常常见,可以回头再看看前面的通用数据类型消化一下这样的技巧.
可是在这里,我却有一点疑问是否需要这么做,因为TValue的定义如下:
(lobject.h)
73 typedef struct lua_TValue {
74 TValuefields;
75 } TValue;
结合TKey的定义可知,似乎这个union实际上表达成这样的定义更为"合适"一些:
typedef struct TKey {
TValue tvk;
struct Node *next;
} TKey;
因为这样已经足以表达TKey所需要的使命:tvk用来存储key的数值,而next用来存储Hash桶中的下一个结点.
可是,在Lua的代码中针对这个数据结构如此"曲折"的定义,实际上是为了对齐并且节省空间的考量.
以上,将Lua表相关的数据结构做了分析.从以上定义可以看到,Lua的表中涉及到存放数据由两个部分组成,一个是数组,一个是Hash.Lua表的数据结构示意图如下所示:
可以看到的时,虽然其中分为数组和Hash两个部分,但是这两部分在分配时都是分配了一块物理上连续的地址作为存储空间.区别在于,Hash桶部分在逻辑上是以next指针串联起了在同一个Hash上的元素地址.
前面讲解了Lua表的数据结构,下面具体来看看相关的算法,这里大体可以分为这几个部分:查找和新增元素.
先来看看查找算法,如果将其他的细枝末节去掉,在Lua表中查找一个数据的伪代码如下:
如果输入的Key是一个正整数,并且它的值 > 0 && <= 数组大小
尝试在数组部分查找
否则尝试在Hash部分进行查找:
计算出该Key的Hash值,根据此Hash值访问node数组得到Hash桶所在位置
遍历该Hash桶下的所有链表元素,直到找到该Key为止
以上可以看出,即使是一个正整数的key,其存储部分也不见得会一定落在数组部分,完全取决于它的大小是否落在了当前数组可容纳的空间范围内,下面的代码为例:
function print_ipairs(t)
for k, v in ipairs(t) do
print(k)
end
end
local t = {}
t[1] = 0
t[100] = 0
print_ipairs(t)
以上代码创建了一个Lua表,向其中添加了key分别为1和100的两条记录,最后通过ipairs打印出其数组部分的key分别是什么,但是最后的输出只有1这一个key,可见100在这里并没有落入数组中.
接下来继续看添加一个新的元素具体的流程,这里比较复杂,因为涉及到重新分配表中数组和Hash部分的流程.需要说明的时,这部分的API,包括luaH_set/luaH_setnum/luaH_setstr三个函数,它们的实际行为,并不在其函数内部对key所对应的数据进行添加或者修改,而是返回根据该key查找到的TValue指针,由外部的使用者来进行实际的替换操作,最典型的例子就是settable这个OpCode了:
(lvm.c)
134 void luaV_settable (lua_State *L, const TValue *t, TValue *key, StkId val) {
135 int loop;
136 for (loop = 0; loop < MAXTAGLOOP; loop++) {
137 const TValue *tm;
138 if (ttistable(t)) { /* `t' is a table? */
139 Table *h = hvalue(t);
140 TValue *oldval = luaH_set(L, h, key); /* do a primitive set */
141 if (!ttisnil(oldval) || /* result is no nil? */
142 (tm = fasttm(L, h->metatable, TM_NEWINDEX)) == NULL) { /* or no TM? */
143 setobj2t(L, oldval, val);
144 luaC_barriert(L, h, val);
145 return;
146 }
147 /* else will try the tag method */
148 }
149 else if (ttisnil(tm = luaT_gettmbyobj(L, t, TM_NEWINDEX)))
150 luaG_typeerror(L, t, "index");
151 if (ttisfunction(tm)) {
152 callTM(L, tm, t, key, val);
153 return;
154 }
155 t = tm; /* else repeat with `tm' */
156 }
157 luaG_runerror(L, "loop in settable");
158 }
这里暂时不展开对该函数的解析,仅关注代码行140-146的几行代码:在通过luaH_set查找到旧的数据(如果该key的数据之前存在)/或新增的数据(如果该key的数据之前不存在),无论何种情况,只要返回的TValue指针不为空,那么都可以使用setobj2t来对返回的数据进行实际的修改操作.可见,Lua表的set类API,其内部并不完成实际的数据赋值操作,而是返回该key所对应的数据TValue指针.
回头继续看Lua表中set类API的流程.首先根据前面提到的查找流程来查找该key对应的数据是否已经存在,如果已经存在了就直接返回TValue指针,由外部调用程序具体进行修改操作.否则,就调用newkey函数新分配一个该key对应的数据:
(ltable.c)
392 /*
393 ** inserts a new key into a hash table; first, check whether key's main
394 ** position is free. If not, check whether colliding node is in its main
395 ** position or not: if it is not, move colliding node to an empty place and
396 ** put new key in its main position; otherwise (colliding node is in its main
397 ** position), new key goes to an empty position.
398 */
399 static TValue *newkey (lua_State *L, Table *t, const TValue *key) {
400 Node *mp = mainposition(t, key);
401 if (!ttisnil(gval(mp)) || mp == dummynode) {
402 Node *othern;
403 Node *n = getfreepos(t); /* get a free place */
404 if (n == NULL) { /* cannot find a free place? */
405 rehash(L, t, key); /* grow table */
406 return luaH_set(L, t, key); /* re-insert key into grown table */
407 }
408 lua_assert(n != dummynode);
409 othern = mainposition(t, key2tval(mp));
410 if (othern != mp) { /* is colliding node out of its main position? */
411 /* yes; move colliding node into free position */
412 while (gnext(othern) != mp) othern = gnext(othern); /* find previous */
413 gnext(othern) = n; /* redo the chain with `n' in place of `mp' */
414 *n = *mp; /* copy colliding node into free pos. (mp->next also goes) */
415 gnext(mp) = NULL; /* now `mp' is free */
416 setnilvalue(gval(mp));
417 }
418 else { /* colliding node is in its own main position */
419 /* new node will go into free position */
420 gnext(n) = gnext(mp); /* chain new position */
421 gnext(mp) = n;
422 mp = n;
423 }
424 }
425 gkey(mp)->value = key->value; gkey(mp)->tt = key->tt;
426 luaC_barriert(L, t, key);
427 lua_assert(ttisnil(gval(mp)));
428 return gval(mp);
429 }
这个函数的功能,划分为以下几个部分.首先,根据key来查找其所在Hash桶的mainposition,如果返回的结果该Node的值为nil,那么直接将key赋值并且返回Node的TValue指针就可以了;否则说明该mainposition位置已经有其他数据了,需要重新分配空间给这个新的key,然后将这个新的Node串联到对应的Hash桶上.可见这里的整个过程都是在Hash部分进行的,理由是即使key是一个数字,也已经在调用newkey函数之前进行了查找,结果是没有找到,所以这个key都会进入到Hash部分来进行查找.
重新分配Lua表空间的代码,比较复杂,可能会涉及到数组和Hash两部分数据的迁移.它的入口函数是rehash函数,整个过程的伪代码列举如下:
首先分配一个位图nums,将其中的所有位置0,这个位图的意义在于:nums数组中第i个元素存放的是key在2^(i-1), 2^i之间的元素数量
遍历lua Table中的数组部分,计算在数组部分中的元素数量,更新对应的nums数组元素数量.(numusearray函数)
遍历lua Table中的Hash部分,因为其中也可能存放了正整数,也根据这里的正整数数量更新对应的nums数组元素数量.(numusehash函数)
此时nums数组已经有了当前这个Table中所有正整数的分配统计,逐个遍历nums数组,获得其范围区间内所包含的整数数量大于50%的最大index,做为rehash之后的数组大小,超过这个范围的正整数,就分配到Hash部分了.(computesizes函数)
根据上面计算得到的调整后的数组和Hash桶大小对Lua表进行调整(resize函数)
对上面的伪代码算法做一下解释.Lua的设计思想,是简单高效,并且还要尽量的节省内存资源.rehash的过程,除了增大Lua表的大小以容纳新的数据之外,还希望能借此机会对原有的数组和Hash部分进行一个调整,让两部分都尽可能发挥其存储的最高容纳效率.那么,这里的标准是什么呢?希望在调整过后,数组在每一个2次方位置,其容纳的元素数量都超过了该范围的50%,能达到这个目标的话,那么Lua认为这个数组范围就发挥了最大的效率.
设想一个场景来模拟一下前面的算法流程,假设现在有一个Lua表,经过了一些变化之后,它的数组有以下key的元素:1,2,3,20.首先,算法将计算这些key(1,2,3,20)都被分配到了哪些区间.在这个算法里使用的是一个数组来保存落在每个范围内的数据数量,这个数组中每个元素的意义是:
nums[i] = number of keys between 2^(i-1) and 2^i
得到的结果是:
nums[0] = 1(1落在此区间)
nums[1] = 1(2落在此区间)
nums[2] = 1(3落在此区间)
nums[3] = 0
nums[4] = 0
nums[5] = 1(20落在此区间)
nums[6] = 0
后面的都是nums[n] = 0了(其中n >= 5 且 n <= MAXBITS)
计算完毕得到这个数组每个元素的数据之后,也就是得到了落在每个范围内的数据数量,来开始计算怎样才能最大限度的使用这部分空间.这个算法由函数computesize实现:
(ltable.c)
189 static int computesizes (int nums[], int *narray) {
190 int i;
191 int twotoi; /* 2^i */
192 int a = 0; /* number of elements smaller than 2^i */
193 int na = 0; /* number of elements to go to array part */
194 int n = 0; /* optimal size for array part */
195 for (i = 0, twotoi = 1; twotoi/2 < *narray; i++, twotoi *= 2) {
196 if (nums[i] > 0) {
197 a += nums[i];
198 if (a > twotoi/2) { /* more than half elements present? */
199 n = twotoi; /* optimal size (till now) */
200 na = a; /* all elements smaller than n will go to array part */
201 }
202 }
203 if (a == *narray) break; /* all elements already counted */
204 }
205 *narray = n;
206 lua_assert(*narray/2 <= na && na <= *narray);
207 return na;
208 }
结合前面的测试数据,来"试运行"一下这个函数,此时传入的narray参数是4,也就是目前数组部分的数据数量. 首先,twotoi为1,i为0,a在循环初始时为0,它表示的时循环到目前为止数据小于2^i的数据数量.
1) i = 0, nums[i] = 1,twotoi = 1, a += nums[i] = 1,此时满足a > twotoi/2,也就是满足这个范围内数组利用率大于50%的原则,记录下这个范围也就是n = twotoi = 1,到目前为止的数据数量na = a = 1
2) i = 1, nums[i] = 1,twotoi = 2, a += nums[i] = 2,此时同样满足a > twotoi/2的条件,继续记录下这个位置和数据数量.
后面的算法依次类推,可以发现当遍历完毕nums数组时,最后一次记录的位置是3,也就是说1,2,3这三个元素落在了数组部分,而20则落在了Hash部分,数组的大小是3.