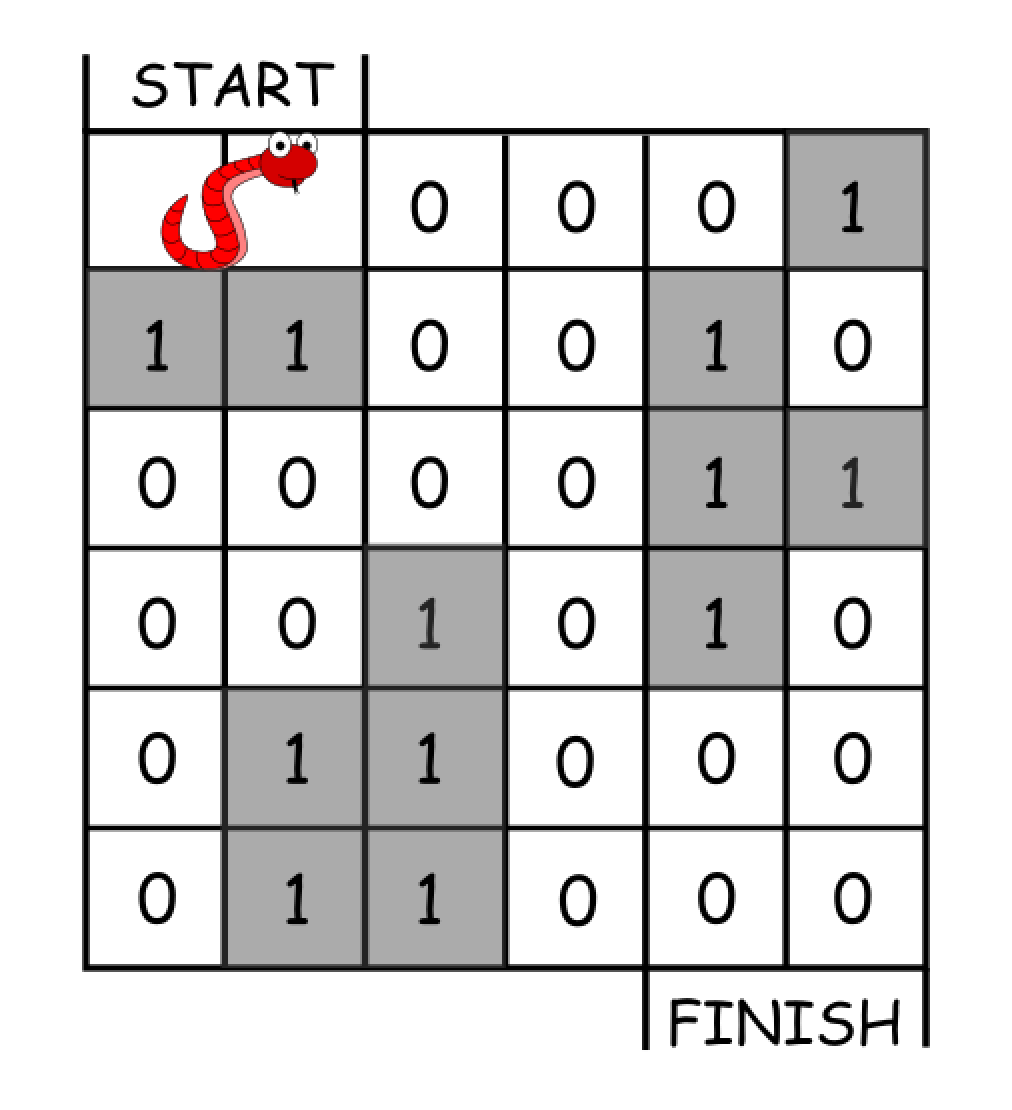
In an n*n grid, there is a snake that spans 2 cells and starts moving from the top left corner at (0, 0) and (0, 1). The grid has empty cells represented by zeros and blocked cells represented by ones. The snake wants to reach the lower right corner at (n-1, n-2) and (n-1, n-1).
In one move the snake can:
- Move one cell to the right if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
- Move down one cell if there are no blocked cells there. This move keeps the horizontal/vertical position of the snake as it is.
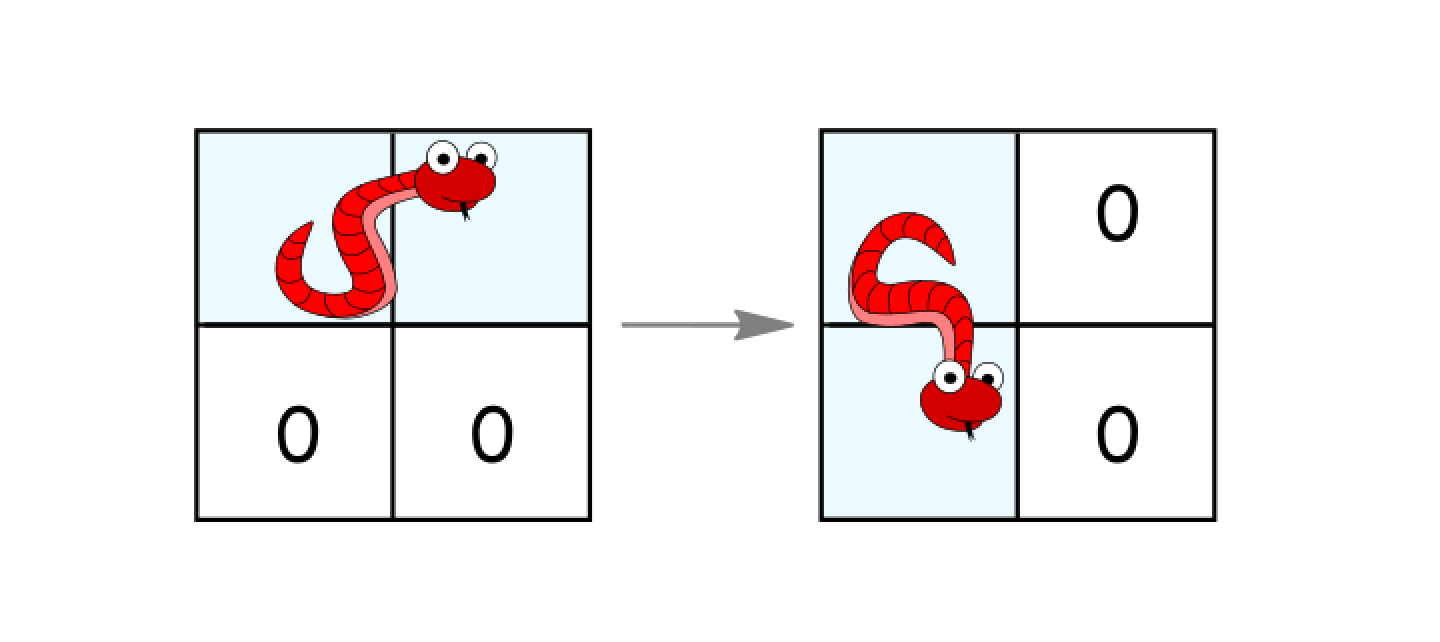
- Rotate clockwise if it's in a horizontal position and the two cells under it are both empty. In that case the snake moves from
(r, c)and(r, c+1)to(r, c)and(r+1, c).
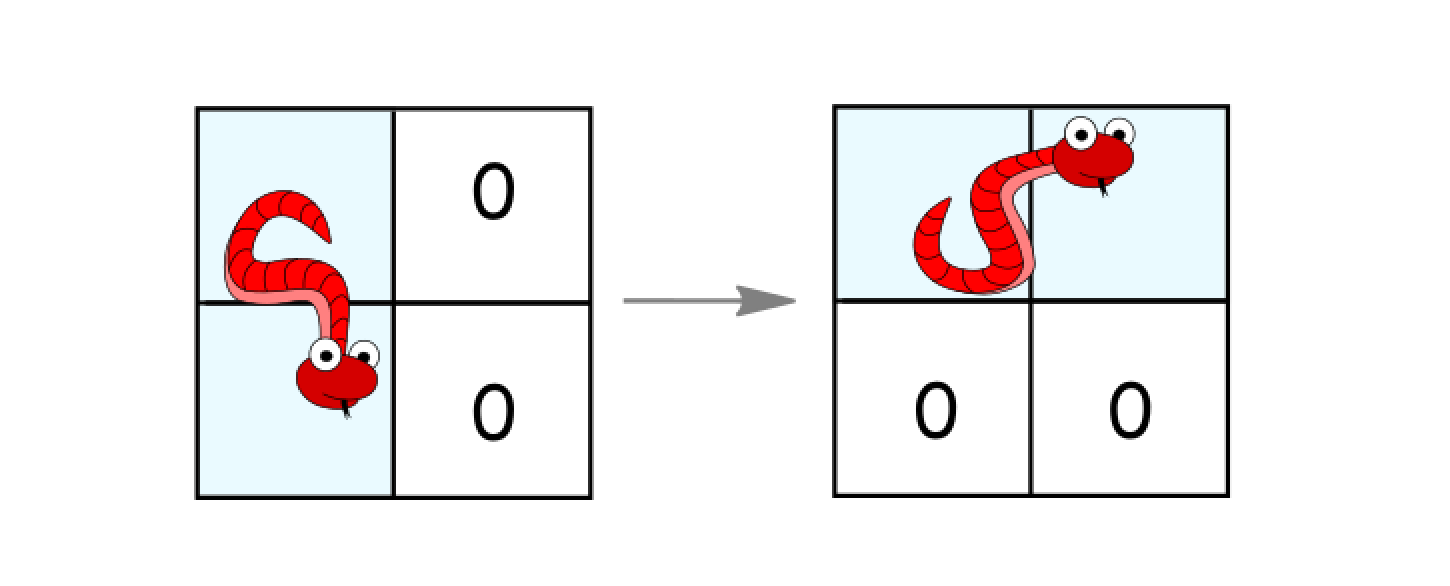
- Rotate counterclockwise if it's in a vertical position and the two cells to its right are both empty. In that case the snake moves from
(r, c)and(r+1, c)to(r, c)and(r, c+1).
Return the minimum number of moves to reach the target.
If there is no way to reach the target, return -1.
Example 1:
Input: grid = [[0,0,0,0,0,1],
[1,1,0,0,1,0],
[0,0,0,0,1,1],
[0,0,1,0,1,0],
[0,1,1,0,0,0],
[0,1,1,0,0,0]]
Output: 11
Explanation:
One possible solution is [right, right, rotate clockwise, right, down, down, down, down, rotate counterclockwise, right, down].
Example 2:
Input: grid = [[0,0,1,1,1,1], [0,0,0,0,1,1], [1,1,0,0,0,1], [1,1,1,0,0,1], [1,1,1,0,0,1], [1,1,1,0,0,0]] Output: 9
Constraints:
2 <= n <= 1000 <= grid[i][j] <= 1- It is guaranteed that the snake starts at empty cells.
BFS.
class Solution:
def minimumMoves(self, grid: List[List[int]]) -> int:
def check(a, b):
if (a, b) not in vis:
vis.add((a, b))
q.append((a, b))
n = len(grid)
target = (n * n - 2, n * n - 1)
q = deque([(0, 1)])
vis = {(0, 1)}
ans = 0
while q:
for _ in range(len(q)):
a, b = q.popleft()
if (a, b) == target:
return ans
i1, j1 = a // n, a % n
i2, j2 = b // n, b % n
if (
j1 + 1 < n
and j2 + 1 < n
and grid[i1][j1 + 1] == 0
and grid[i2][j2 + 1] == 0
):
check(i1 * n + j1 + 1, i2 * n + j2 + 1)
if j1 == j2:
check(a, i1 * n + j2 + 1)
if (
i1 + 1 < n
and i2 + 1 < n
and grid[i1 + 1][j1] == 0
and grid[i2 + 1][j2] == 0
):
check((i1 + 1) * n + j1, (i2 + 1) * n + j2)
if i1 == i2:
check(a, (i2 + 1) * n + j1)
ans += 1
return -1class Solution {
public int minimumMoves(int[][] grid) {
int n = grid.length;
int[] target = new int[] {n * n - 2, n * n - 1};
Deque<int[]> q = new ArrayDeque<>();
q.offer(new int[] {0, 1});
boolean[][] vis = new boolean[n * n][n * n];
int ans = 0;
vis[0][1] = true;
while (!q.isEmpty()) {
for (int k = q.size(); k > 0; --k) {
int[] p = q.poll();
if (p[0] == target[0] && p[1] == target[1]) {
return ans;
}
int a = p[0], b = p[1];
int i1 = a / n, j1 = a % n;
int i2 = b / n, j2 = b % n;
if (j1 + 1 < n && j2 + 1 < n && grid[i1][j1 + 1] == 0 && grid[i2][j2 + 1] == 0) {
check(i1 * n + j1 + 1, i2 * n + j2 + 1, q, vis);
if (j1 == j2) {
check(a, i1 * n + j2 + 1, q, vis);
}
}
if (i1 + 1 < n && i2 + 1 < n && grid[i1 + 1][j1] == 0 && grid[i2 + 1][j2] == 0) {
check((i1 + 1) * n + j1, (i2 + 1) * n + j2, q, vis);
if (i1 == i2) {
check(a, (i2 + 1) * n + j1, q, vis);
}
}
}
++ans;
}
return -1;
}
private void check(int a, int b, Deque<int[]> q, boolean[][] vis) {
if (!vis[a][b]) {
vis[a][b] = true;
q.offer(new int[] {a, b});
}
}
}class Solution {
public:
int minimumMoves(vector<vector<int>>& grid) {
int n = grid.size();
vector<int> target = {n * n - 2, n * n - 1};
queue<vector<int>> q;
q.push({0, 1});
vector<vector<bool>> vis(n * n, vector<bool>(n * n));
int ans = 0;
vis[0][1] = true;
while (!q.empty()) {
for (int k = q.size(); k; --k) {
auto p = q.front();
if (p == target) return ans;
q.pop();
int a = p[0], b = p[1];
int i1 = a / n, j1 = a % n;
int i2 = b / n, j2 = b % n;
if (j1 + 1 < n && j2 + 1 < n && grid[i1][j1 + 1] == 0 && grid[i2][j2 + 1] == 0) {
check(i1 * n + j1 + 1, i2 * n + j2 + 1, q, vis);
if (j1 == j2) check(a, i1 * n + j2 + 1, q, vis);
}
if (i1 + 1 < n && i2 + 1 < n && grid[i1 + 1][j1] == 0 && grid[i2 + 1][j2] == 0) {
check((i1 + 1) * n + j1, (i2 + 1) * n + j2, q, vis);
if (i1 == i2) check(a, (i2 + 1) * n + j1, q, vis);
}
}
++ans;
}
return -1;
}
void check(int a, int b, queue<vector<int>>& q, vector<vector<bool>>& vis) {
if (!vis[a][b]) {
vis[a][b] = true;
q.push({a, b});
}
}
};func minimumMoves(grid [][]int) int {
n := len(grid)
target := []int{n*n - 2, n*n - 1}
q := [][]int{{0, 1}}
vis := make([][]bool, n*n)
for i := range vis {
vis[i] = make([]bool, n*n)
}
vis[0][1] = true
ans := 0
check := func(a, b int) {
if !vis[a][b] {
vis[a][b] = true
q = append(q, []int{a, b})
}
}
for len(q) > 0 {
for k := len(q); k > 0; k-- {
p := q[0]
q = q[1:]
if p[0] == target[0] && p[1] == target[1] {
return ans
}
a, b := p[0], p[1]
i1, j1 := a/n, a%n
i2, j2 := b/n, b%n
if j1+1 < n && j2+1 < n && grid[i1][j1+1] == 0 && grid[i2][j2+1] == 0 {
check(i1*n+j1+1, i2*n+j2+1)
if j1 == j2 {
check(a, i1*n+j2+1)
}
}
if i1+1 < n && i2+1 < n && grid[i1+1][j1] == 0 && grid[i2+1][j2] == 0 {
check((i1+1)*n+j1, (i2+1)*n+j2)
if i1 == i2 {
check(a, (i2+1)*n+j1)
}
}
}
ans++
}
return -1
}