4. Applying boundary conditions in Florence

In this section we will have a look on how to set up and apply essential and natural boundary conditions in Florence. Applying boundary conditions in Florence is facilitated through callback functions.

a) Applying essential/Dirichlet boundary conditions

Consider the following square domain meshed with quadrilateral elements showing node and element numbering.

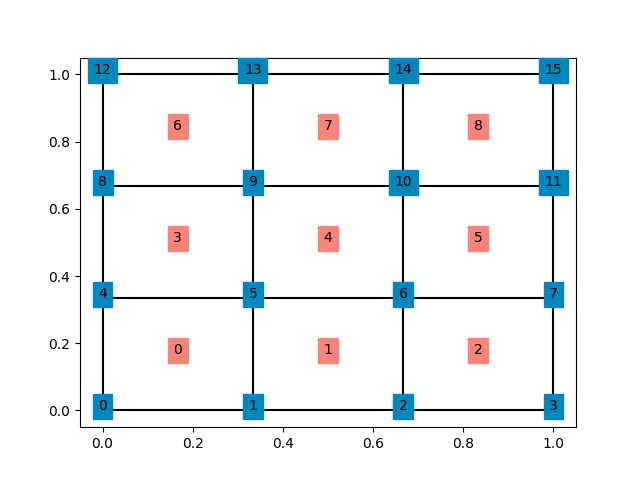
We would now like to apply the Dirichlet boundary conditions such that all nodes at (x=0) are fixed in x and y direction. To do this we need need first create our own function

def dirichlet_function(mesh):
    pass

The name of this function can be chosen arbitrarily and does not need to be dirichlet_function. Within the body of this function, we need to create an array of NaNs of size nnode x nvar where nnode is the number of nodes in the domain and nvar is the number of variable/DoFs per node. For Poisson type problems nvar=1, for structural mechanics problems nvar=ndim (where ndim is the the spatial dimension i.e. ndim=2 for 2D/plane strain/plane stress problems and ndim=3 for 3D problems) and electromechanics problems nvar=ndim+1.

def dirichlet_function(mesh):
    boundary_data = np.zeros((mesh.nnode,2)) + np.NAN

Now, to fix all nodes at (x=0) in x and y directions we can simply query using numpy which nodes lie at x=0 i.e. mesh.points[:,0]==0 or np.isclose(mesh.points[:,0],0.)

def dirichlet_function(mesh):
    boundary_data = np.zeros((mesh.nnode,2)) + np.NAN
    condition = np.isclose(mesh.points[:,0],0.)

If we wanted to fix all nodes at (y=0) then the function would have looked like

def dirichlet_function(mesh):
    boundary_data = np.zeros((mesh.nnode,2)) + np.NAN
    condition = np.isclose(mesh.points[:,1],0.)

Notice that 0 has changed to 1 in mesh.points