-
Notifications
You must be signed in to change notification settings - Fork 16
4. Applying boundary conditions in Florence
In this section we will have a look on how to set up and apply essential and natural boundary conditions in Florence. Applying boundary conditions in Florence is facilitated through callback functions.
Consider the following square domain meshed with quadrilateral elements showing node and element numbering.
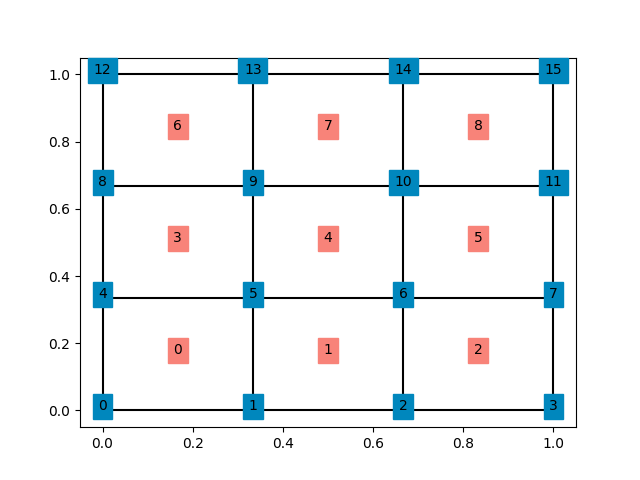
Let us assume that we are solving an elasticity type problem and we would now like to apply the Dirichlet boundary conditions such that all nodes at (x=0) are fixed in x and y direction. To do this we need to first create our own function
def dirichlet_function(mesh):
passThe name of this function can be chosen arbitrarily and does not need to be dirichlet_function. Within the body of this function, we need to create an array of NaNs of size nnode x nvar where nnode is the number of nodes in the domain and nvar is the number of variable/DoFs per node. For Poisson type problems nvar=1, for structural mechanics problems nvar=ndim (where ndim is the the spatial dimension i.e. ndim=2 for 2D/plane strain/plane stress problems and ndim=3 for 3D problems) and electromechanics problems nvar=ndim+1.
def dirichlet_function(mesh):
boundary_data = np.zeros((mesh.nnode,2)) + np.NANNow, to fix all nodes at (x=0) in x and y directions we can simply query using numpy which nodes lie at x=0 i.e. mesh.points[:,0]==0 or np.isclose(mesh.points[:,0],0.)
def dirichlet_function(mesh):
boundary_data = np.zeros((mesh.nnode,2)) + np.NAN
condition = np.isclose(mesh.points[:,0],0.)If we wanted to fix all nodes at (y=0) then the function would have looked like
def dirichlet_function(mesh):
boundary_data = np.zeros((mesh.nnode,2)) + np.NAN
condition = np.isclose(mesh.points[:,1],0.)Notice that 0 has changed to 1 in mesh.points. Finally we are supposed to return the data from our function that is
def dirichlet_function(mesh):
boundary_data = np.zeros((mesh.nnode,2)) + np.NAN
condition = np.isclose(mesh.points[:,0],0.)
return boundary_data;We now need to tell Florence to use this boundary condition for our mesh
boundary_condition = BoundaryCondition()
boundary_condition.SetDirichletCriteria(dirichlet_function,mesh)Here, we initiate a boundary condition object of Florences and call its method SetDirichletCriteria by giving it our function name dirichlet_function followed by the arguments that our function takes. In principle, our function can take as many arguments as needed.
Applying nodal natural/Neumann boundary condition is exactly the same as applying Dirichlet boundary condition. the only difference is in telling Florence how to use it
boundary_condition = BoundaryCondition()
boundary_condition.SetNeumannCriteria(neumann_function,mesh)Applying Neumann boundary condition on a face/region or even a curved region is also supported. In such case, we still need our user defined function, but we need to return two arrays from our function, one array of size mesh.faces.shape[0] and the other one of size mesh.faces.shape[0] x ndim. The first array will describe which mesh faces the boundary condition should be applied on. The second array describes the forces applied to each of those elements. Please refer to the hyperelastic explicit dyanmics example in Florence's main repository for an example of this type of boundary condition.