Differential equations often give rise to rank-structured matrices characterized by low-rank off-diagonal blocks. These matrices can be conveniently represented in a hierarchical format, enabling efficient arithmetic operations such as fast matrix-vector multiplication. Among these, hierarchical matrices [2] form a class of dense rank-structured matrices with a hierarchical low-rank off-diagonal block structure. Such matrices frequently emerge in applications like the finite element discretization of elliptic partial differential equations (PDEs), radial basis function interpolation, and boundary integral equations. A prominent example of hierarchical matrices is the Hierarchical Off-Diagonal Low-Rank (HODLR) matrix, which is constructed by hierarchically partitioning the matrix using a binary cluster tree. At each level of the tree, all off-diagonal blocks are represented as low-rank matrices, enabling efficient storage and computation.
Leveraging low-precision arithmetic has become increasingly important in computational mathematics due to its potential to reduce data communication, energy consumption, and storage requirements. According to the IEEE floating-point standard, single-precision arithmetic can achieve up to twice the speed of double precision on certain hardware, while half-precision arithmetic can offer up to a fourfold speedup. The trade-offs between precision and computational accuracy are critical when designing algorithms for high-performance computing.
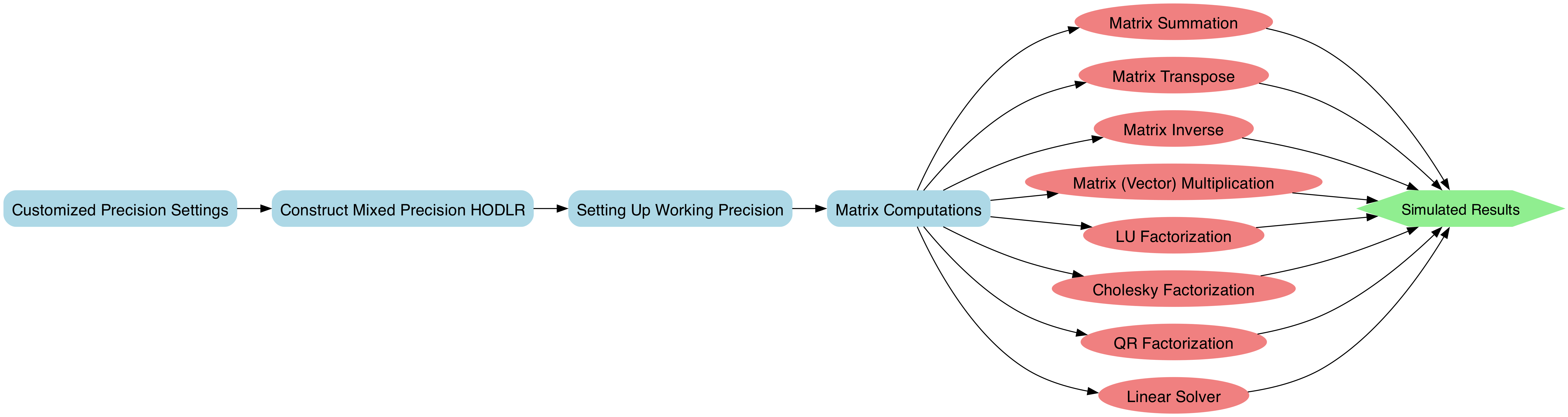
The mhodlr software repository addresses this by providing tools to evaluate and optimize precision requirements for HODLR matrix construction. By simulating various levels of precision, the software allows users to assess reconstruction errors and computational errors associated with HODLR matrix operations. The repository also offers a user-friendly API for constructing HODLR matrices and performing basic matrix computations, facilitating simulations for mixed-precision and adaptive-precision arithmetic in HODLR matrix computing [1]. The low-precision arithmetic simulations employed in this work are based on the methodologies described in [4], ensuring both accuracy and efficiency.
Our software mainly contains three modules
| Class | Description |
|---|---|
@hodlr |
Compute HODLR matrix |
@mphodlr |
Compute HODLR matrix in mixed precision (precisions are defined by the users) |
@amphodlr |
Compute HODLR matrix in adaptive precision (precisions are provided by the users) |
The environment for running mhodlr is MATLAB2023a, MATLAB2023b, MATLAB2024a, MATLAB2024b.
One can fork this repository, and simply download this repository via
git clone https://github.com/<username>/mhodlr.gitThen add the destination folder where mhodlr is installed to MATLAB’s search path:
addpath('mhodlr/mhodlr')Simple example on usage is referred to EXAMPLE.
| Matrix computations | API |
|---|---|
| Matrix summation | add(A, B, ...) |
| Matrix substraction | sub(A, B, ...) |
| Matrix transpose | H.transpose() |
| Matrix inverse | inverse(H) |
| Matrix (vector) multiplication | dot(A/H, H/B, ...), mdot(A/H, H/B, ...) |
| LU factorization | hlu(H/A), mhlu(H/A) |
| Cholesky factorization | hchol(H/A), mhchol(H/A) |
| QR factorization | hqr(H, method), mhqr(H, method) |
| Triangular solver (Lower triangular solver LX=B, Upper triangular solver XU=B) | htrsl(H, B), htrsu(B, H) |
| Linear solver (Ax = b) | lu_solve(H, B) qr_solve(method, H, B) |
mhodlr enables multiple precision control for matrix computation based on HODLR representation. It allows users to control the precision in a global environment, without the need to specify the precision everytime when the function is called.
The precision setting is performed by
u = precision('h'); % or ther precision customization
set_prec(u);Then all the HODLR arithmetic function starting with ''m'' will performed in precision u.
Any forms of contributions are welcomed. Our documents are still in progress; feel free to pull request and submit issues for suggestions. Before contributing code, we suggest to contact the maintainers. The contact information of maintainers can be found in MaintainerList.
This project is supported by the European Union (ERC, InEXASCALE, 101075632). Views and opinions expressed are those of the authors only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them.
[1] C. Erin, X. Chen and X. Liu, Mixed precision HODLR matrices, arXiv:2407.21637, (2024), https://doi.org/10.48550/arXiv.2407.21637.
[2] S. B¨orm, L. Grasedyck, and W. Hackbusch, Introduction to hierarchical matrices with applications, Eng. Anal. Bound. Elem., 27 (2003), pp. 405–422, https://doi.org/10.1016/S0955-7997(02)00152-2.
[3] N. J. Higham and S. Pranesh, Simulating low precision floating-point arithmetic, SIAM J. Sci. Comput., 41 (2019), pp. C585–C602, https://doi.org/10.1137/19M1251308.