logistic_regression_matlab

Logistic Regression

1. View the dataset

2. Sigmoid function

function g = sigmoid(z)
  g = ones(size(z))./(1 + exp(-z));
end

3. Cost function and gradient descent

J = mean((-y).* log(sigmoid(X*theta))- (1-y).* log(1 - sigmoid(X*theta)));
grad = 1/m * X' * (sigmoid(X*theta) - y);

4. Learning Theta using fminunc

MATLAB's fminunc is an optimization solver that finds the minimum of an uncinstrained function. fminunc input:

• The initial value of the parameters we are trying to optimize
• A funtion computes the cost function and gradient

% Set options for fminunc
options = optimset('GradObj', 'on', 'MaxIter', 400);
% Run fminunc to obtain the optimal theta
% This function will return theta and the cost
[theta, cost] = ...
fminunc(@(t)(costFunction(t, X, y)), initial theta, options);

'GradObj', 'on': set fminunc that our function returns both the cost and the gradient. This allows fminunc to use the gradient when minimizing the function.

'MaxIter', 400: set fminunc run for at most 400 steps before it terminates.

@(t) ( costFunction(t, X, y) ): specify the actual function we are minimizing, creates a function, with argument t, which calls your costFunction.

5. Trainig result and decision boundary

Regularized Logistic Regression

1. View the dataset

2. High order polynomial feature mapping

% Inputs X1, X2 must be the same size
% Returns a new feature array with more features, comprising of 
% X1, X2, X1.^2, X2.^2, X1*X2, X1*X2.^2, etc..
degree = 6;
out = ones(size(X1(:,1)));
for i = 1:degree
    for j = 0:i
        out(:, end+1) = (X1.^(i-j)).*(X2.^j);
    end
end

3. Cost function and gradient

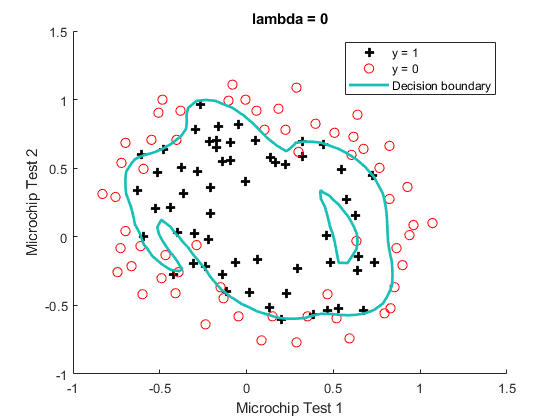
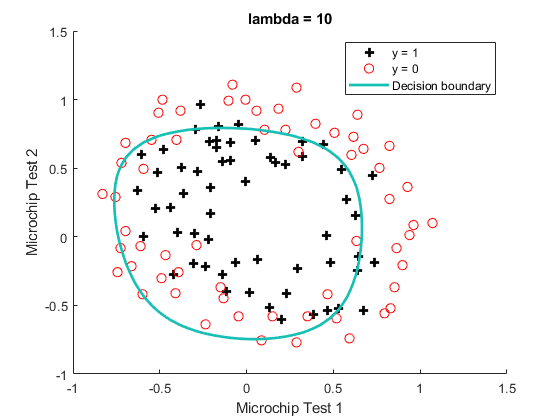
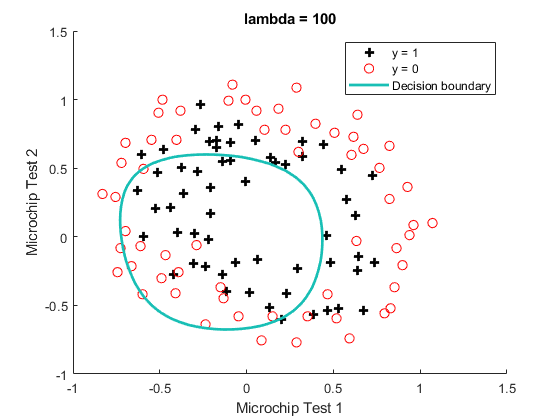
theta0 = [0; theta(2:end)];
J = mean((-y).* log(sigmoid(X*theta))- (1-y).* log(1 - sigmoid(X*theta)))...
    + lambda/(2*m)*sum(theta0.*theta0);
grad = 1/m * X' * (sigmoid(X*theta) - y) + lambda/m*theta0;

4. Learning Theta using fminunc

% Set Options
options = optimset('GradObj', 'on', 'MaxIter', 400);
% Optimize
[theta, J, exit_flag] = ...
  fminunc(@(t)(costFunctionReg(t, X, y, lambda)), initial_theta, options);

5. Decision boundary with different regularization

lambda = 1 (just right)

lambda = 0 (no regularization - overfitting)

lambda = 10 (too much regularization - underfitting)

lambda = 100 (too much regularization - underfitting)