Unsupervised class discovery is a data mining method to identify unknown possible groups (clusters) of items solely based on intrinsic features and no external variables. Basically, clustering includes four steps:
I use a dataset coming from an RNA-seq experiment on 476 patients with non-muscle invasive bladder cancer. To make this tutorial reproducible, clinical data can be downloaded from this repo, and normalized RNA-seq data can be obtained through this link. So if you are willing to use these materials, start your analysis from feature selection section onward.
In this step, we need to filter out incomplete cases and low expressed genes, then transforming/normalizing gene expression values. Usually, the analysis would start from a raw count matrix coming from an RNA-seq experiment. I keep those genes that have an expression in 10% of samples with a count of 10 or higher. All missing values must be removed or one needs to impute their value if one wants to keep them. In my dataset, there is no missing value.
For transformation/normalization I use variance stabilizing transformation (VST) implemented as vst function from DESeq2 packages which at the same time will normalize the raw count also. Using other types of transformation like Z score, and log transformation are also quite common. If the expression matrix contains estimated transcript counts (like RSEM) or counts normalized for sequencing depth (like FPKM) , log2 transformation of the values would prepare the data for clustering. See the following examples:
-
Using log2(RSEM) gene expression value and removing genes with NA values of more than 10% across samples. Then select the top 25% most-varying genes by the standard deviation of gene expression across samples (A. Gordon Robertson et al., Cell,2017).
-
Using FPKM matrix and keeping genes with (log2(FPKM+1)>2 in at least 10% of samples and selecting a subsets (2K, 4K, 6K ) of MAD ranked genes to identify stable classes (Jakob Hedegaard et al, Cancer Cell, 2016).
Feature selection: Because there are a large number of features (genes) in the expression matrix, a feature selection step should be done to limit the analysis to those genes that possibly explain variation between samples in the cohort. So it is recommended to select features for clustering. I select 2k, 4k, and 6k top genes based on median absolute deviation (MAD) . A number of other methods like "feature selection based on the most variance", "feature dimension reduction and extraction based on Principal Component Analysis (PCA)", and "feature selection based on Cox regression model" could be applied, as well. To read more see the bioconductor package CancerSubtypes manual.
#_________________________________reading data and processing_________________________________#
# reading count data
rna <- read.table("Uromol1_CountData.v1.csv", header = T, sep = ",", row.names = 1)
head(rna[1:5, 1:5], 5)
# U0001 U0002 U0006 U0007 U0010
#ENSG00000000003.13 1458 228 1800 3945 293
#ENSG00000000005.5 0 0 9 0 0
#ENSG00000000419.11 594 23 792 1378 139
#ENSG00000000457.12 548 22 1029 976 148
#ENSG00000000460.15 53 2 190 136 47
dim(rna)
# [1] 60483 476 This is a typical output from hts-seq count matrix with more than 60,000 genes
# Dissecting dataset based on gene-type
library(biomaRt)
mart <- useDataset("hsapiens_gene_ensembl", useMart("ensembl"))
genes <- getBM(attributes= c("ensembl_gene_id","hgnc_symbol", "gene_biotype"),
mart= mart)
# see gene types returned by biomaRt
data.frame(table(genes$gene_biotype))[order(- data.frame(table(genes$gene_biotype))[,2]), ]
# We will continue with protein-coding here:
rna <- rna[substr(rownames(rna),1,15) %in% genes$ensembl_gene_id[genes$gene_biotype == "protein_coding"],]
dim(rna)
#[1] 19581 476 These are protein-coding genes
# Reading associated clinical data
clinical.exp <- read.table("uromol_clinic.csv", sep = ",", header = T, row.names = 1)
head(clinical.exp[1:5,1:5], 5)
# UniqueID CLASS BASE47 CIS X12.gene.signature
#U0603 U0603 luminal luminal no-CIS high_risk
#U0497 U0497 luminal basal no-CIS low_risk
#U0839 U0839 luminal luminal CIS low_risk
#U1043 U1043 luminal luminal no-CIS high_risk
#U0566 U0566 luminal basal no-CIS low_risk
# Make sure about sample order in rna and clincal.exp dataset
all(rownames(clinical.exp) %in% colnames(rna))
#[1] TRUE
all(rownames(clinical.exp) == colnames(rna))
#[1] FALSE
# reordering rna dataset
rna <- rna[, rownames(clinical.exp)]
#______________________ Data transformation & Normalization ______________________________#
library(DESeq2)
dds <- DESeqDataSetFromMatrix(countData = rna,
colData = clinical.exp,
design = ~ 1) # 1 passed to the function because of no model
# pre-filteration, however while using DESeq2 package it is not necessary, because the function automatically will filter out low-count genes
# Keeping genes with expression in 10% of samples with a count of 10 or higher
keep <- rowSums(counts(dds) >= 10) >= round(ncol(rna)*0.1)
dds <- dds[keep,]
# vst transformation
vsd <- assay(vst(dds)) # For a fully unsupervised transformation one can set blind = TRUE (which is the default).
#_________________________________# Feature Selection _________________________________#
# top 5K based on MAD
mads=apply(vsd,1,mad)
# check data distribution
hist(mads, breaks=nrow(vsd)*0.1)
# selecting features
mad2k=vsd[rev(order(mads))[1:2000],]
#mad4k=vsd[rev(order(mads))[1:4000],]
#mad6k=vsd[rev(order(mads))[1:6000],]
Clustering is about grouping similar samples into one cluster and keeping them far from dissimilar samples based on distance measures. There is a diverse list of dissimilarity matrix calculation methods (distance measures). To see a list of available distance measures please check ?stats::dist and ?vegan::vegdist(). The latter needs to have the vegan package to be installed:
- For log-transformed gene expression, Euclidean-based measures can be applied.
- For RNA-seq normalized counts, correlation-based measures (Pearson, Spearman) or a Poisson-based distance can be used.
Clustering algorithms: To see a list of algorithms please check diceR package vignettes. The most widely used algorithms are partitional clustering and hierarchical clustering.
Partitional clustering are clustering method used to classify samples into multiple clusters based on their similarity. The algorithms are required to specify the number of clusters to be generated. The commonly used partitional clustering includes:
- K-means clustering (KM): Each cluster is represented by the center or means of the data points belonging to the cluster. This method is sensitive to outliers.
- K-medoids clustering or PAM (Partitioning Around Medoids), in which, each cluster is represented by one of the objects in the cluster. PAM is less sensitive to outliers.
Hierarchical clustering (HC) In contrast to partitional clustering, this method does not require pre-specifying the number of clusters to be generated. HC can be grouped into two classes.
- Agglomerative:"bottom-up" approach, each observation is initially considered as a cluster of its own (leaf), and pairs of clusters are merged as one moves up the hierarchy.
- Divisive: "top-down" approach, This begins with the root so all observations start in one cluster, and splits are performed recursively as one moves down the hierarchy.
Some words on how to compute distances between clusters: Indeed there are different ways to do cluster agglomeration (i.e., linkage ). When one uses stat package, possible methods include “ward.D”, “ward.D2”, “single”, “complete”, “average”, “mcquitty”, “median” or “centroid”. Generally, complete linkage and Ward’s method are preferred. More reading materials on this can be found here. As a result, hierarchical clustering provides a tree-based representation of the objects, which is also known as a dendrogram.
In practice, HC, KM, and PAM are commonly used for gene expression data.
To quantitatively determine the number and membership of possible clusters within the dataset, I will use the Consensus Clustering (CC) approach. Applying this method has proved to be effective in new cancer subclass discoveries. For more information on the methodology please refer to the seminal paper by Monti et al. (2003) and ConsensusClusterPlus package manual.
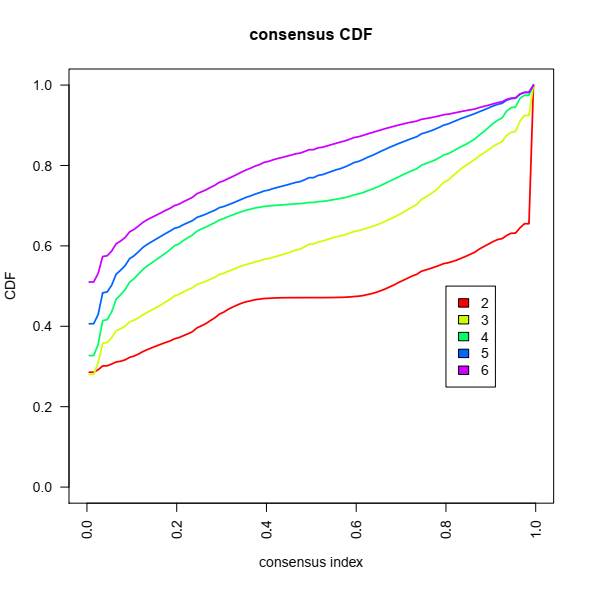
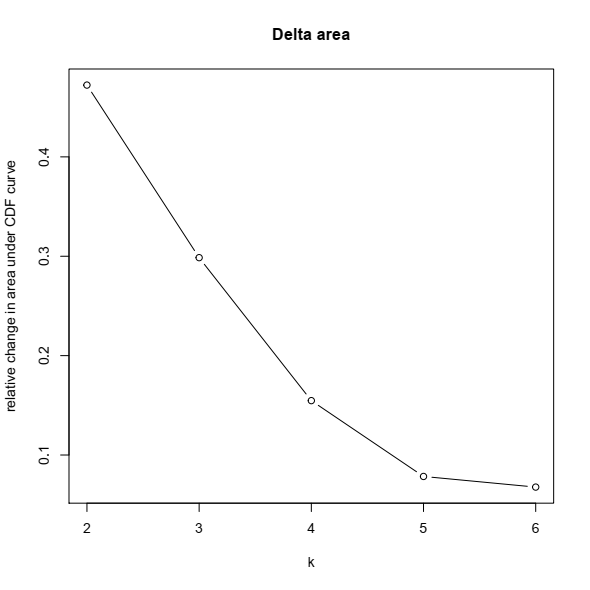
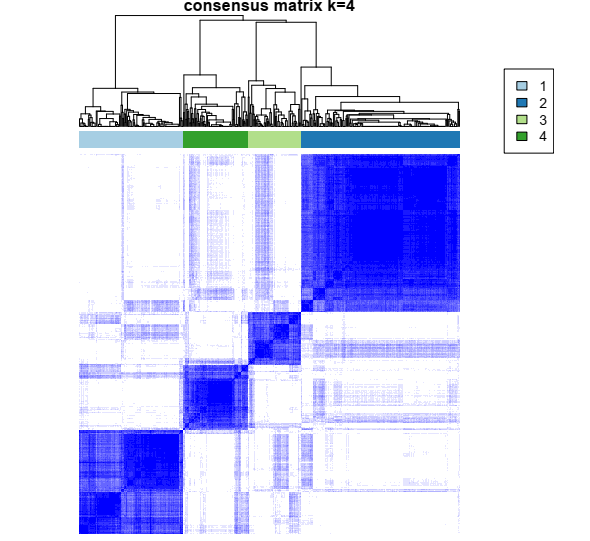
To determine the number of clusters based on CC, there are several graphics that would help to this extent. (1) A Color-coded heatmap corresponding to the consensus matrix that represents consensus values from 0–1; white corresponds to 0 (never clustered together) and dark blue to 1 (always clustered together). (2) Consensus Cumulative Distribution Function (CDF) plot, This graphic lets one determine at what number of clusters,k, the CDF reaches an approximate maximum. So consensus and cluster confidence are at a maximum at this k. (3) Based on the CDF plot, a chart for the relative change in area under the CDF curve can be plotted. This plot allows a user to determine the relative increase in consensus and determine k at which there is no appreciable increase.
#_________________________________# Clustering & Cluster assignment validation _________________________________#
# Finding optimal clusters by CC
library(ConsensusClusterPlus)
results = ConsensusClusterPlus(mad2k,
maxK=6,
reps=50,
pItem=0.8,
pFeature=1,
title= "geneExp",
clusterAlg="pam",
distance="spearman",
seed=1262118388.71279,
plot="pdf")For this post, I selected 80% item resampling (pItem), 80% gene resampling (pFeature), and a maximum evaluated k of 6 so that cluster counts of 2,3,4,5,6 are
evaluated (maxK), 50 resamplings (reps), partition around medoids algorithm (clusterAlg) Spearman correlation distances (distance), gave
the output a title (title), and asked to have graphical results written to a pdf plot file. I also set a random seed so that this example is repeatable
(seed).
The above command returns several plots, helpful to make decisions about cluster number, especially plots showing consensus CDF and relative change in area under CDF curve.
So by looking at the plots, the optimal number of clusters would be four in this case. Below is a consensus plot of samples when k = 4. Results for other k values can be found in the result pdf file. This is not in agreement with the original paper, where the authors reported three subtypes. However, in a new report from the same group using a new pipeline they concluded that NMIBC has four different subtypes! ref.
Assessing cluster assignment or cluster validation indicates to the procedure of assessing the goodness of clustering results. Alboukadel Kassambara has published a detailed post on this topic. In this tutorial, I will use the Silhouette method for cluster assessment. this method can be used to investigate the separation distance between the obtained clusters. The Silhouette plot reflects a measure of how close each data point in one cluster is to a point in the neighboring clusters. This measure, Silhouette width, has a range of -1 to +1. Value near +1 shows that the sample is far away from the closest data point from a neighboring cluster. A negative value may indicate wrong cluster assignment and a value close to 0 means an arbitrary cluster assignment to that data point.
Since by clustering, one should expect to find clusters of samples that are significantly different in terms of survival probability, here as a kind of assessing cluster assignment in biological perspective, I perform survival analysis between clusters (subtypes) to see significant differences, if any.
The output of ConsensusClusterPlus is a list, and the result for each of k values like k = 4, can be accessed by results[[4]]. I save the result in a new object and then will move forward with calculating and then plotting the Silhouette plot.
#_________________________________#Assessing cluster assignment _________________________________#
#Silhouette width analysis
cc4 = results[[4]]
# calcultaing Silhouette width using the cluster package
library(cluster)
cc4Sil = silhouette(x = cc4[[3]], # x is a numeric vector that indicates cluster assignment for each data point
dist = as.matrix(1- cc4[[4]])) # dist should be a distance matrix and NOT a similarity matrix, so I subtract the matrix from one to get that dist matrix
#For visualization:
library(factoextra)
fviz_silhouette(cc4Sil, palette = "jco",
ggtheme = theme_classic())The above function returns a summary of the Silhouette width for each cluster:
cluster size ave.sil.width
1 1 130 0.75
2 2 199 0.83
3 3 66 0.65
4 4 81 0.72From the below image, one can get an idea of the average Silhoutte width as well as the size of each cluster.
#_________________________________#Assessing cluster assignment _________________________________#
#Survival analysis
### Preparing dataset for survival analysis
cc4Class = data.frame(cc4$consensusClass)
cc4Class$ID = rownames(cc4Class)
cc4Class = data.frame(cc4Class[match(rownames(clinical.exp),cc4Class$ID),])
all(cc4Class$ID == rownames(clinical.exp))
# new encoding for status, time, and cluster
clinical.exp$status = ifelse(clinical.exp$Progression.to.T2. == "NO", 0,1)
clinical.exp$time = as.numeric(clinical.exp$Progression.free.survival..months. * 30)
clinical.exp$cluster = as.factor(cc4Class$cc4.consensusClass)
library(survival)
res.cox <- coxph(Surv(time, status) ~ cluster, data = clinical.exp)
res.coxCall:
coxph(formula = Surv(time, status) ~ cluster, data = clinical.exp)
coef exp(coef) se(coef) z p
cluster2 -1.47638 0.22846 0.48357 -3.053 0.00226
cluster3 0.22532 1.25272 0.42213 0.534 0.59351
cluster4 -2.39949 0.09076 1.03301 -2.323 0.02019
Likelihood ratio test=21.88 on 3 df, p=6.908e-05
n= 476, number of events= 31 summary(res.cox)Call:
coxph(formula = Surv(time, status) ~ cluster, data = clinical.exp)
n= 476, number of events= 31
coef exp(coef) se(coef) z Pr(>|z|)
cluster2 -1.47638 0.22846 0.48357 -3.053 0.00226 **
cluster3 0.22532 1.25272 0.42213 0.534 0.59351
cluster4 -2.39949 0.09076 1.03301 -2.323 0.02019 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
exp(coef) exp(-coef) lower .95 upper .95
cluster2 0.22846 4.3771 0.08855 0.5894
cluster3 1.25272 0.7983 0.54769 2.8653
cluster4 0.09076 11.0175 0.01198 0.6874
Concordance= 0.714 (se = 0.039 )
Likelihood ratio test= 21.88 on 3 df, p=7e-05
Wald test = 16.52 on 3 df, p=9e-04
Score (logrank) test = 22.14 on 3 df, p=6e-051- Biostar posts: https://www.biostars.org/p/321773/ https://www.biostars.org/p/225315/ https://www.biostars.org/p/74223/ https://www.biostars.org/p/281161/ https://www.biostars.org/p/273107/
2- https://www.datanovia.com/en/courses/partitional-clustering-in-r-the-essentials/
3- https://2-bitbio.com/2017/10/clustering-rnaseq-data-using-k-means.html