Goldbach's conjecture states that every even integer n greater than 2 is the sum of two primes. It has not been proved, but has been confirmed by computer for n up to 4 � 10^18 by T. Oliveira e Silva.
This project contains computational experiments regarding Goldbach's conjecture. We're certainly not going to try to prove or disprove Goldbach's conjecture. But we will try to learn a bit of Haskell and see what interesting patterns we can find for as large of values of n as our computational power will allow.
This project is my implementation of "A Golden Prime Project" from Keeping it R.E.A.L.: Research Experiences for All Learners by Carla D. Martin and Anthony Tongen.
Rather than write the prime generation code in Haskell myself, I decided to concentrate on code related specifically to Goldbach's conjecture in this project. Hence I've used Kees Doets' and Jan van Eijck's Sieve of Erastothenes Haskell implementation from The Haskell Road to Logic, Maths and Programming. This code is in TUOLP.hs.
(I've written my own prime generation code in C in my a-prime-project.)
It should be noted that the "time complexity of calculating all primes below n in the random access machine model is O(n log log n) operations".
I first find all pairs of primes that sum to n for a given even number n > 2.
My first implementation does the obvious thing:
primePairs' :: Integer -> [(Integer, Integer)]
primePairs' n = [(p, q) | p <- takeWhile (< n) primes, q <- takeWhile (< n) primes, p <= q, p + q == n]
This clearly runs in quadratic time if you ignore the calls to primes.
Here is the performance data:
n primePairs' computation time (sec)
256 0.008
512 0.024
1,024 0.069
2,048 0.226
4,096 0.058
8,192 0.262
16,384 1.123
32,768 5.335
65.536 44.821
131,072 245.860
262,144 1211.950
524,288 4887.736
(Note that my performance measuring code isn't the most scientific in the world, which is why the computation time for 2048 is less than the computation time for 4096. But, whatever.)
There is an obvious linear time implementation:
primePairsHelper :: Integer -> [Integer] -> [(Integer, Integer)]
primePairsHelper n ps
| length ps == 0 = []
| length ps == 1 && head ps + head ps == n = [(head ps, head ps)]
| head ps + last ps < n = primePairsHelper n (tail ps)
| head ps + last ps > n = primePairsHelper n (init ps)
| otherwise = (head ps, last ps) : primePairsHelper n (tail (init ps))
primePairs :: Integer -> [(Integer, Integer)]
primePairs n = primePairsHelper n (takeWhile (< n) primes)
These functions can be found in AGPP.hs.
However, the speed-up is disappointing:
n primePairs' computation time (sec) primePairs computation time (sec)
256 0.008 0.001
512 0.024 0.001
1,024 0.069 0.004
2,048 0.226 0.018
4,096 0.058 0.080
8,192 0.262 0.247
16,384 1.123 1.161
32,768 5.335 5.175
65,536 44.821 43.395
131,072 245.860 242.805
262,144 1,211.950 1,168.571
524,288 4,887.736 4,806.134
1,048,576 NA 22,614.785
For small n, the speed-up is dramatic. But it's not small n that I'm worried about as far as performance goes. Taking into account the O(n log log n) running time of the Sieve of Erastothenes primes routine, we get the following running times:
primePairs': O(n^2) * O(n log log n) = O(n^3 log log n)
primePairs: O(n) * O(n log log n) = O(n^2 log log n)
So what is going on here? primePairs should be a lot faster than
primePairs'. My best guess is that for large n, the Sieve of
Erastothenes table is taking up a lot of memory, and, hence, there is a
possibly a lot of memory swapping out to disk. This is causing the time
of the calls to primes to dominate the computation time. That's my
guess at any rate. It would be interesting to compare these relative
times on computers with different amounts of RAM or to monitor at which
values of n virtual memory starts being used.
At any rate, depending on your definition of reasonable, the highest
even number we can reasonably enter into our primePairs function is
somewhere between 2^15 (32,768) and 2^20 (1,048,576). This means we
certainly can't reproduce Silva's results, but that's not the point of
this exercise.
We next examine the number of pairs of primes that sum to a particular even number. Recall that, if Goldbach's conjecture is true, this will always be at least 1 (for n > 2). The code for generating this can be found in AGPP.hs and PrintPairCounts.hs.
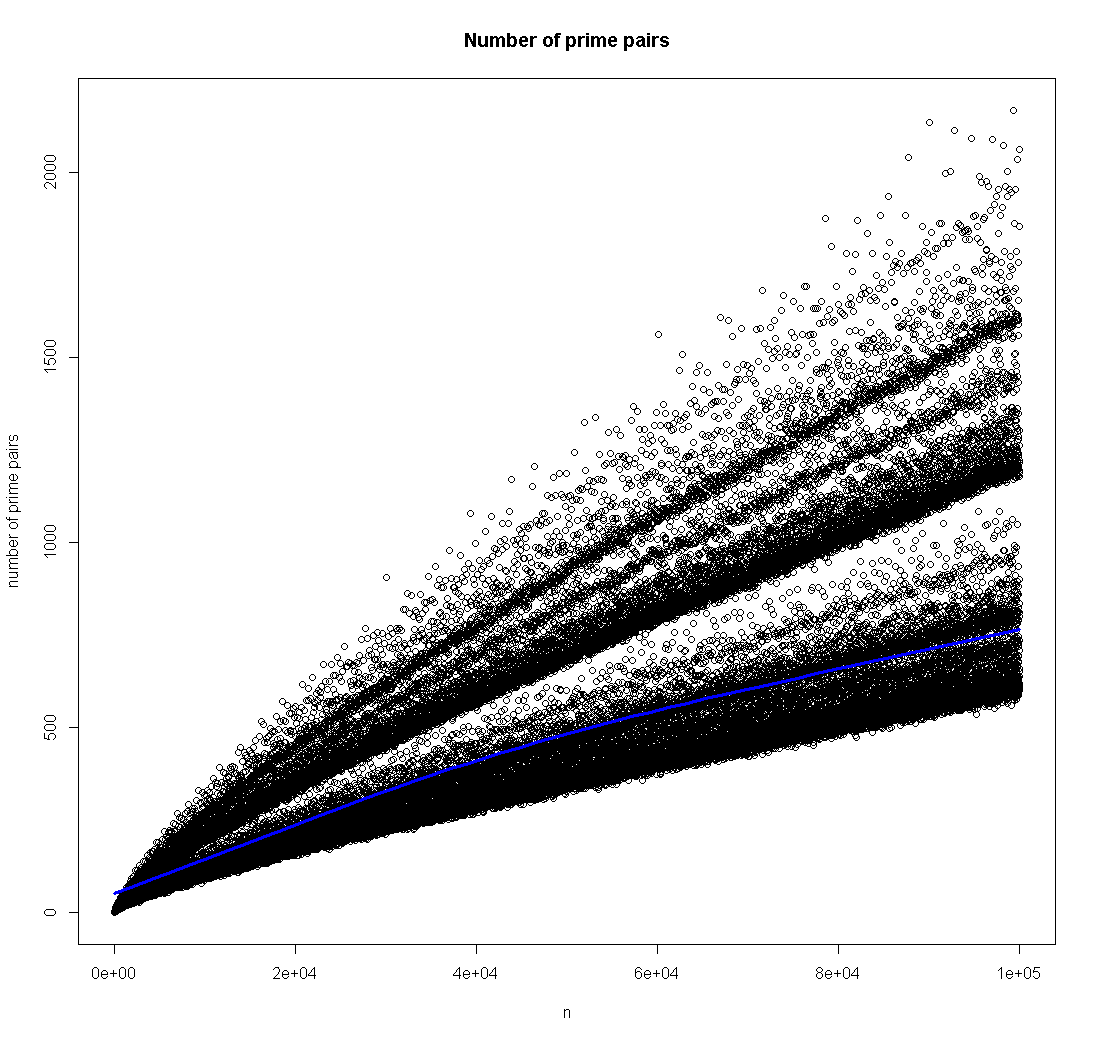
We plot the results.
Note that we've added a LOESS smoothing line in blue. Of course, if this plot were ever to touch the x-axis, then Goldbach's conjecture would not be true. Of course we also know that this is not going to happen for n up to 4 � 10^18 because of Silva's work.
Now there is something interesting in this data. Note the curve gathered near the LOESS curve, but notice that there is a second gathering of points above this and perhaps a third gathering of points above that! What the heck is that?!
From our plots, it certainly seems reasonable to believe the Goldbach conjecture. It's hard to imagine that curve suddenly dropping all the way to the x-axis. Of course, this doesn't prove anything.
What's interesting is to color these points using the number of prime divisors of each number.
prime.pair.count <- read.csv("./data/triples100000.csv")
colnames(prime.pair.count) <- c("n", "count", "divisors")
plot(
prime.pair.count$n, prime.pair.count$count,
col=c("red","blue", "green", "yellow", "cyan", "magenta")[prime.pair.count$divisors],
main="Number of prime pairs", xlab="n", ylab="number of prime pairs")
For even numbers between 4 and 100,000, how many even numbers only have one pair of distinct pairs of primes adding to it? How many evens have exactly two distinct pairs of primes adding to it? Exactly three? Four? Higher?
table(prime.pair.count$divisors)
##
## 1 2 3 4 5 6
## 14 11488 23796 12951 1724 25
hist(
prime.pair.count$divisors, main="Number of pairs for n < 100,000",
xlab="Number of pairs")