Also known as Gravity sort, this algorithm was inspired from natural phenomenons and was designed keeping in mind objects(or beads) falling under the influence of gravity.
The Idea: Positive numbers are represented by a set of beads like those on an abacus.
* Bead sort algorithm ! (or gravity Sort)
* Class Sorting algorithm
* Data structure Array
* Worst-case performance О(s) , S is the sum of the input integers
* Best-case performance O(1)
* Average performance O(n^1/2), In a realistic physical model that uses gravity,
* Worst-case space complexity
* where n is the size of the input array.
* ans S S is the sum of the input integers.
* Note: The algorithm’s run–time complexity ranges from O(1) to O(S) (S is
* the sum of the input integers) depending on the user’s perspective.
* Finally, three possible implementations are suggested.
*
* Author: Pooya HatamiIf you are using a browser, you can download node-sort-bead.js from GitHub or just bellow hotlink to it:
<script src="https://raw.githubusercontent.com/pooyahatami/Algorithm-Sort-Bead/master/node-sort-bead.js"></script>If you are using node, you can install node-sort-bead with npm.
npm install node-sort-bead
var nodesort = require('./node-sort-bead');
var displaymode = "No"; //"Yes"; // "Yes" for more details of algorithm progress
...
nodesort(inputArray, displaymode, function(err,sortRef) {
if (err) {
// TODO error handeling
}
else {
var result = sortRef.beadSort(inputArray);
//var result = sortRef.gravitySort(inputArray);
// TODO output
}
});- Sort Array of integers between 0 and rangeMax
- Array's element could not be negative.
- Returns error mesage if not found valid input.
- Turn On details of Algorithms progress useing : displaymode = "Yes"
var displaymode = "No"; //"Yes";var nodesort = require('./node-sort-bead');
var displaymode = "No"; //"Yes"; // "Yes" for more details of algorithm progress
var base = 10;
var arrin00 = [20, 8 , -11, 12, 22 , 9 , 10 ];
var arrin01 = [20, 8 , 48, 120, 220 , 390 , 1000 ];
var arrin02 = [20, 8 , 480 , 120, 220 , 390 , 1000 ];
var arrin03 = [1120, 800 , 480 , 120, 20 , 390 , 1000 ];
var arrin04 = ['g', 'e', 'e', 'k', 's', 'f', 'o',
'r', 'g', 'e', 'e', 'k', 's'];
var arrin05 = [1, 3, 7, 25, 12, 9, 8,
121, 221, 10, 18, 29, 49];
var arrin06 = [1, 3, -7, 25, 12, 9, 8,
121, 221, -10, 18, 29, 49];
var arrin07 = [1, 3, 7000000000000000000, 25, 12, 9, 8,
121, 221, 100000000000000000000000000 , 18, 290000000000000000000, 49];
var arrin08 = [1, 3, 75432, 25, 12, 9, 8,
121, 221, 976562 , 18, 299999, 49];
var arrin09 = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434 , 0.611 , 0.621 ];
var arrin10 = [1,342, 14,293 , 0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434 , 0.611 , 0.621 ];
var arrin11 = [5, 8 , 11, 12, 2 , 9 , 10 , 4 , 11, 10, 12, 7, 9 ];
var arrin12 = "";
//var arrin13 = [A7,02,22,77,37,15,00,40,B00,75,04,05,07,75,52,12,50,77,71,D07]; //base16
var arrin14 = [1001,101010,11,10,01,111,100,1000,11100,10110,101,100010,0111,101,11111,1000001,1,0,111,11010]; //base 2
var arrin15 = [7,2,22,77,37,15,10770,740,70,75,04,5,107,75,52,12,50,177,71,207]; //base 8
var arrin16 = [7,2,3,15,19,12,10,4,8,11,007,5,00017,6,9,12,1,13,18,20]; // smal numbers for bead sort
function solveSorting(inputArray) {
var arr_original = inputArray.toString() ;
var sortedArray = inputArray;
nodesort(inputArray, displaymode, function(err,sortRef) {
if (err) {
console.log(err);
}
else {
//var result = sortRef.beadSort(inputArray);
var result = sortRef.gravitySort(inputArray);
console.log("Success attempt to sort array \r\n \t ["+arr_original+" ] \r\n and result is : \r\n \t [ "
+ result + " ]" );
sortedArray = result;
}
console.log("----------------------------------------------------------");
});
return sortedArray;
};
solveSorting(arrin16);
solveSorting(arrin01);
solveSorting(arrin00);
solveSorting(arrin03);
solveSorting(arrin11);
solveSorting(arrin12);
solveSorting(arrin14);
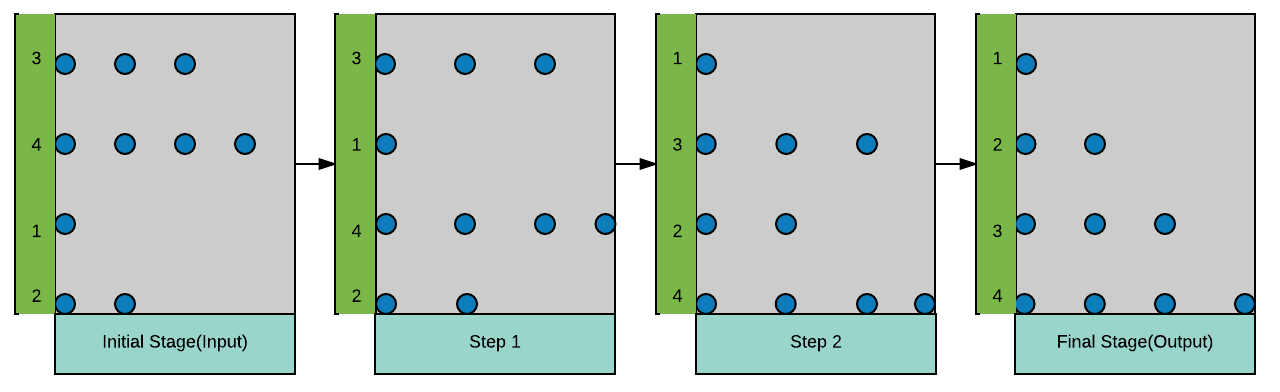
solveSorting(arrin15);Sorting of {7, 2, 1, 4, 2} using Bead Sort. Beads fall down one by one if there is space below.
Like in the image above the beads represent the following numbers from top to bottom : 7, 2, 1, 4, 2. Now, imagine that this is the position of the beads at time t = 0 and with every passing second the beads will fall down by one level provided there is no bead already present below them. In such a case, they just rest upon the bead below them.(Rods are numbered from left to right and levels are numbered from the bottom as 1, 2, ………. n.) Now, at time t = 1 the bottom 2 beads in the first two rods from the left stay at their positions while the second bead from the top from the second rod comes down by one level to rest upon the bead below it. The beads in the 3rd and 4th rod at level 2 come down to level 1. Simultaneously, the beads in the rods 3 to 7 come down by one level. Now, the numbers from top to bottom become: 2, 6, 2, 2, 4. This goes on till time t = 4 where we get the sorted sequence of numbers from top to bottom which is: 1, 2, 2, 4, 7.
Why is it called so?
When one tries to visualize this algorithm it appears as if beads are falling down under the influence of gravity to the bottom-most level they can reach resulting the set of beads being arranged in a descending order from the ground up. If you are having trouble visualizing this visit this link
Lets say that we have to sort the numbers 3, 4, 1, 2. The above algorithm would work like this.
Let us understand it with the help of an example.
Original, unsorted list:
170, 45, 75, 90, 802, 24, 2, 66
Sorting by least significant digit (1s place) gives: [*Notice that we keep 802 before 2, because 802 occurred before 2 in the original list, and similarly for pairs 170 & 90 and 45 & 75.]
170, 90, 802, 2, 24, 45, 75, 66
Sorting by next digit (10s place) gives: [*Notice that 802 again comes before 2 as 802 comes before 2 in the previous list.]
802, 2, 24, 45, 66, 170, 75, 90
Sorting by most significant digit (100s place) gives:
2, 24, 45, 66, 75, 90, 170, 802**Time Complexity:*8
The algorithm’s run–time complexity ranges from O(1) to O(S) (S is the sum of the input integers) depending on the user’s perspective. Finally, three possible implementations are suggested.
O(1) : Dropping all beads together as a single (simultaneous) operation. This complexity cannot be implemented in practice. O(n^1^/^2): In a realistic physical model that uses gravity, the time it takes to let the beads fall is proportional to the square root of the maximum height, which is proportional to n. O(n) : Dropping the row of beads in the frame (representing a number) as a distinct operation since the number of rows is equal to n. O(S) : Dropping each and every bead’ as a separate operation since S is the sum of all the beads. Like the Pigeonhole sort, bead sort is unusual in that in worst case it can perform faster than O(n log n), the fastest performance possible for a comparison sort in worst case. This is possible because the key for a bead sort is always a positive integer and bead sort exploits its structure.
Space Complexity: Bead sort is the record-holder as for waste. The costs for the extra memory exceed the costs for storing the array itself. Its memory complexity is O(n^2)
Implementation of Bead Sort Following is a simple C++ implementation of Radix Sort.
// C++ program to implement gravity/bead sort
#include <bits/stdc++.h>
using namespace std;
#define BEAD(i, j) beads[i * max + j]
// function to perform the above algorithm
void beadSort(int *a, int len)
{
// Find the maximum element
int max = a[0];
for (int i = 1; i < len; i++)
if (a[i] > max)
max = a[i];
// allocating memory
unsigned char beads[max*len];
memset(beads, 0, sizeof(beads));
// mark the beads
for (int i = 0; i < len; i++)
for (int j = 0; j < a[i]; j++)
BEAD(i, j) = 1;
for (int j = 0; j < max; j++)
{
// count how many beads are on each post
int sum = 0;
for (int i=0; i < len; i++)
{
sum += BEAD(i, j);
BEAD(i, j) = 0;
}
// Move beads down
for (int i = len - sum; i < len; i++)
BEAD(i, j) = 1;
}
// Put sorted values in array using beads
for (int i = 0; i < len; i++)
{
int j;
for (j = 0; j < max && BEAD(i, j); j++);
a[i] = j;
}
}
// driver function to test the algorithm
int main()
{
int a[] = {5, 3, 1, 7, 4, 1, 1, 20};
int len = sizeof(a)/sizeof(a[0]);
beadSort(a, len);
for (int i = 0; i < len; i++)
printf("%d ", a[i]);
return 0;
}Following is a simple Java implementation of Bead Sort.
// Bead sort Java implementation
public class BeadSort
{
public static void main(String[] args)
{
BeadSort now=new BeadSort();
int[] arr=new int[(int)(Math.random()*11)+5];
for(int i=0;i<arr.length;i++)
arr[i]=(int)(Math.random()*10);
System.out.print("Unsorted: ");
now.display1D(arr);
int[] sort=now.beadSort(arr);
System.out.print("Sorted: ");
now.display1D(sort);
}
int[] beadSort(int[] arr)
{
int max=0;
for(int i=0;i<arr.length;i++)
if(arr[i]>max)
max=arr[i];
//Set up abacus
char[][] grid=new char[arr.length][max];
int[] levelcount=new int[max];
for(int i=0;i<max;i++)
{
levelcount[i]=0;
for(int j=0;j<arr.length;j++)
grid[j][i]='_';
}
/*
display1D(arr);
display1D(levelcount);
display2D(grid);
*/
//Drop the beads
for(int i=0;i<arr.length;i++)
{
int num=arr[i];
for(int j=0;num>0;j++)
{
grid[levelcount[j]++][j]='*';
num--;
}
}
System.out.println();
display2D(grid);
//Count the beads
int[] sorted=new int[arr.length];
for(int i=0;i<arr.length;i++)
{
int putt=0;
for(int j=0;j<max&&grid[arr.length-1-i][j]=='*';j++)
putt++;
sorted[i]=putt;
}
return sorted;
}
void display1D(int[] arr)
{
for(int i=0;i<arr.length;i++)
System.out.print(arr[i]+" ");
System.out.println();
}
void display1D(char[] arr)
{
for(int i=0;i<arr.length;i++)
System.out.print(arr[i]+" ");
System.out.println();
}
void display2D(char[][] arr)
{
for(int i=0;i<arr.length;i++)
display1D(arr[i]);
System.out.println();
}
}
/* This code is contributed by Pooya Hatami*/Following is a simple Python implementation of Bead Sort.
# Python program for implementation of Bead Sort
# This code is contributed by Pooya HatamiOutput:
1 1 1 3 4 5 7 20
- Selection Sort
- Bubble Sort
- Insertion Sort
- Merge Sort
- Heap Sort
- QuickSort
- Counting Sort
- Radix Sort
- Bead Sort
- Bucket Sort
- ShellSort